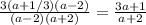
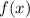необходимо найти ноли производной 
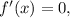т.е. точки, где у функции будет экстремум, и показать, что до экстремума функция 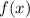падает, т.е. производная 
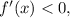а после экстремума функция растёт, т.е. производная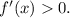 
;
;
;
;
;
;
;
;
;
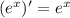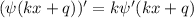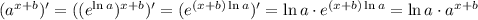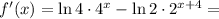
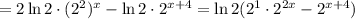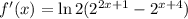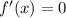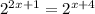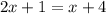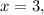причём это единственный корень.
например при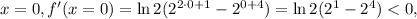 
т.е. функция убывает.
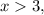например при 
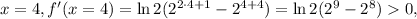т.е. функция растёт.
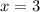как раз достигается минимум: 
;
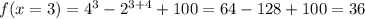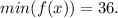
5 - √7 7+√ 5 √7 +√5
= 36(5 + √7) + 88(7-√ 5) - 4(√7- √5) =
(5 - √7) (5+ √7) (7+√ 5)(7-√ 5) (√7 +√5)(√7- √5)
= 36(5 + √7) + 88(7-√ 5) - 4(√7- √5) =
5² - √7² 7² -√ 5² √7² - √5²
= 36(5 + √7) + 88(7-√ 5) - 4(√7- √5) =
25 - 7 49 - 5 7 - 5
= 36(5 + √7) + 88(7-√ 5) - 4(√7- √5) =
18 44 2
= 2(5 + √7) + 2(7-√ 5) - 2 (√7- √5) =
1 1 1
= 2(5 + √7) + 2(7-√ 5) - 2 (√7- √5) =
= 10 + 2√7 + 14 - 2√ 5 - 2√7 + 2√5 = 10 + 14 = 24