Объяснение:
Нам даны несколько уравнений вида
P(t)=at²+bt+c. Т.е. многочлен второй степени от какой-нибудь переменной,t,x,m,n в принципе любые)
Дискриминант считается как
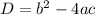 а корни квадратного многочлена находятся по формуле
а корни квадратного многочлена находятся по формуле
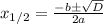 если D>0, то у нас 2 различных корня, если D=0, то у нас 2 совпадающих корня x1=x2, если же D<0, то корней на мн-ве действительных чисел нет, т.к. корни из отрицательных чисел мы пока извлекать не научились. А теперь пользуемся формулой
если D>0, то у нас 2 различных корня, если D=0, то у нас 2 совпадающих корня x1=x2, если же D<0, то корней на мн-ве действительных чисел нет, т.к. корни из отрицательных чисел мы пока извлекать не научились. А теперь пользуемся формулой
1)D=2²-4*1*(-24)=4+96=100(√D=10>0)
x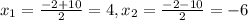
3)D=(-9)²-4*10*2=81-80=1(√D=1>0)
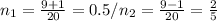
8)D=100-148=-48<0, следовательно корней у уравнения нет.
3) заметим, что (4х-1)(4х+1)=16x²-1, а (3х-5)²=9x²-30x+25, тогда
9x²+16x²-30x+25-1-29=0
25x²-30x-5=0 разделим уравнение на 5,
5x²-6x-1=0
D=36+20=56(√D=2√14>0)
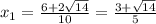
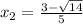
последнее я уже говорил, что один корень уравнение имеет, когда дискриминант равен 0
D=m²-4*12*3=m²-12²=(m-12)(m+12)
D=0⇔(m-12)(m+12)=0⇔m=±12
Например,
В школе, чтобы не возникало путаницы, принято вводить понятие арифметический квадратный корень.И только его используют в школьном курсе математики.
Арифметическим квадратным корнем из числа а называется НЕОТРИЦАТЕЛЬНОЕ число, квадрат которого равен а.
Cамо выражение под знаком корня тоже должно быть неотрицательным, т.к. при возведении в квадрат хоть неотрицательного, хоть отрицательного числа всё равно получим неотрицательное (то есть либо положительное, либо ноль).
При решении квадр. уравнений второй отрицательный корень получаем из тех соображений, что минус пишется перед корнем, а сам корень неотрицателен.
Проверка.