Решим дискриминант и после этого сделаем метод интервала.
x²-3x-4 < 0
Дискриминант:
x²-3x-4 = 0
D = b²-4ac => (-3)²-4*1*(-4) = 9+16 = 25 > 0, 2 корня.
√25 = 5 (можно и в уме)
x =
x₁ =
x₂ =
Корни уравнения: (x+1)(x-4)
На графике будет выглядеть так:
-∞ + - + +∞
00>
-1 4 x
Воспользуемся методом интервала, чтобы понять, в какое направление пойдёт решение:
f (x) = (x+1)(x-4)
f (2) = (2+1)(2-4) = 3*(-2) = -6
ответ: (-∞;-1) ∪ (4;+∞).
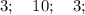
Объяснение:
6) Так как произведение корней принимает положительное значение, то и сами корни принимают положительные значения ⇒ подкоренные выражения также положительны.
ОДЗ:
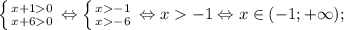
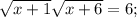
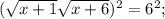
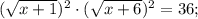
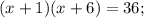
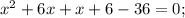
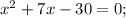
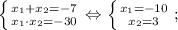
Корень x₁ не удовлетворяет ОДЗ.
7) Знаменатель дроби не равен нулю ⇒ подкоренное выражение строго больше 0. Подкоренное выражение правой части уравнения также строго больше 0, поскольку, в противном случае, значение числителя равно 0, отсюда выходит, что "х" принимает отрицательное значение, что противоречит ОДЗ подкоренного выражения знаменателя дроби.
ОДЗ:
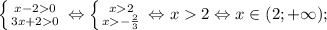
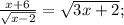

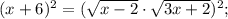

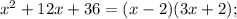
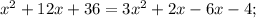
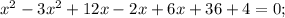
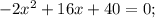
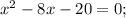
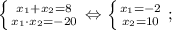
Корень x₁ не удовлетворяет ОДЗ.
8) ОДЗ:

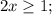
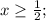
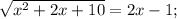
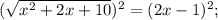
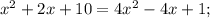
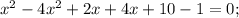
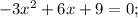
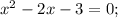
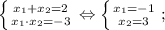
Корень x₁ не удовлетворяет ОДЗ.
{2*x-3*y=-18
Решение:
1. Из первого уравнения данной системы выражаем переменную х. Имеем x= (12 -2*y);
2. Подставляем это выражение во второе уравнение, получаем 2*x-3*y=-18; 2*(12 -2*y) – 3*y = -18; 24 – 4y – 3*y = -18;
3. Решаем полученное линейное равнение: 24 – 4y – 3*y =-18; 24-7*y =-18; -7*y = -42; y=6;
4. Подставляем полученный результат в выражение, полученное в первом пункте. x= (12 -2*y); x=12-2*6 = 0; x=0;
5. Проверяем полученное решение, для этого подставляем найденные числа в исходную систему.{x+2*y =12;
{2*x-3*y=-18;{0+2*6 =12;
{2*0-3*6=-18;{12 =12;
{-18=-18;
Получили верные равенства, следовательно, мы правильно нашли решение.
ответ: (0,6)