Объяснение:
Сумма 1+3+...+(2n-1) значит сумму всех нечетных натуральных чисел начиная с 1 и заканчивая 2n-1
Так как при n=1 =>2n-1=2*1-1=1, то для базы индукции сумма начинается с 1 и ею же заканчивается, т.е. состоит только из одного числа 1,
а уже при n=2 (1+3), n=3 (1+3+5) и т.д., и больше будет два и больше слагаемых, и последний член предстанет "более явно",
при n=1 : 1+3+...+(2n-1) =1=(2n-1)
формула 2n-1 показывает какой вид имеет n-ое слагаемое суммы, но в случае n=1 сумма состоит из одного единственного слагаемого 1
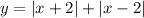
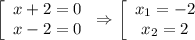
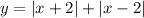параллельный прямой 
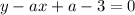если угловые коэффициенты будут совпадать, т.е.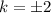 
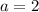- минимальны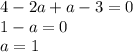й.
и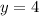 
, получим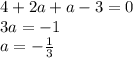
у=7/х
Для определения координат точек пересечения нужно приравнять правые части обоих уравнений найти значения "х" при которых выполняется равенство, затем найденные х подставить в одно из уравнений (удобнее по расчетам в первое) и найти значения у соответствующие этим значениям.
Полученные пары х и у и будут координатами точек пересечения.
Предварительно можно сказать, что первый график - прямая, проходящая через начало координат, а второй гипербола находящаяся в первом и третьем квадрантах.
4х=7/х, 4х^2=7, x 1,2 = +- √7 /2, x1=√7 /2, x2= -√7 /2
y=4x
y1=4*x1=2√7
y2=4*x2= -2√7
Т.о. координаты точек пересечения графиков:
х1= √7 /2 у1=2√7
х2= -√7 /2 у2= -2√7