По Виету х=4; х=-1/2; (х-4)(х+1/2)≤0
-1/24
+ - +
х∈[-1/2;4] Целые 0; 1;2;3;4.
2. х<1/7
2(x-1)(x+1/2)≤0
___-1/21
+ - +
пересечением множеств
(-∞;1/7)∩[-1/2;1]=[-1/2;1/7)
3. неравенство равносильно системе
х²(3-х)(х-4)²≤0
х≠4
034
+ + - -
x∈[-3;4)∪(4;+∞)∪{0}
4. найдем пересечение решений неравенств решением первого служит х∈(-∞;+∞), т.к. дискриминант меньше нуля. он равен 9-16=7, решением второго (х-4)*(х+4)≤0
-44
+ - +
х∈[-4;4] есть х∈[-4;4]
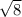x3= корень из 4.5 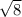x4= минус корень из 4.5
2)(х+2)(х-6)
Подробно так подробно)))
Пример первый:
1) -x^2+4x-3=0 (умножим всё уравнение на (-1))
2) x^2-4x+3=0 - дальше действуем по замечанию(если a+b+c=0, то
Получаем
Теперь раскладываем на множители: (х-
Выходит (х-1)(х+3)
ответ:...
Пример второй:
0,5^2-2x-6=0(умножаем на 2, что-бы потом решать по Теореме Виета)
1x^2-4x-12=0 Т.В.
(х+2)(х-6) - Это ответ...
Удачи в решениях подобных задач