ответ: скорость победителя=12км/ч
Объяснение: пусть скорость 2-го велосипедиста=х, тогда скорость 1-го=х+4. Второй велосипедист потратил на дорогу 96/х времени, а первый 96/х+4. Первый велосипедист потратил времени на 4 меньше, чем второй на дорогу. Составим уравнение:
(96/х)-96(х+4)=4 | находим общий знаменатель: х(х+4)
(96х+384-96х)/х(х+4)=4
384/х²+4х=4 |перемножим числитель и знаменатель соседних дробей крест накрест:
4(х²+4х)=384 |÷4
х²+4х=96
х²+4х-96=0
Д=16-4×(-96)=16+384=400
х1=( -4-20)/2= -24/2= -12
х2=(-4+20)/2=16/2=8
Итак у нас есть 2 значение х, но х1= -12 нам не подходит поскольку скорость не может быть отрицательной поэтому используем х2=8.
Скорость второго велосипедиста=8км/ч, тогда скорость первого=8+4=12км/ч
Т. максимума – х = 15
Объяснение:
Для начала найдём производную функции, чтобы определить промежутки монотонности функции.
Производная (у/g)' = ((y)' × g - (g)' × y)/g², (x)' = 1, (x² + 225)' = 2x, поэтому производная функции = (15 - х)(15 + х)/(х² + 225)² (процесс разложения см. на фотографии).
Критических точек у этой производной не будет, т. к. (х² + 225)² > 0 при любых х, стационарные точки – х = -15, х = 15. Отмечаем их на координатной прямой, обозначаем интервалы, подставляем значения из каждого интервала в производную, чтобы определить её знак на них, и уже исходя из знаков ( "-" – убывание, "+" – возрастание) определяем, убывает или возрастает сама функция. Та точка, в которой возрастание сменяется убыванием, и будем максимумом функции.
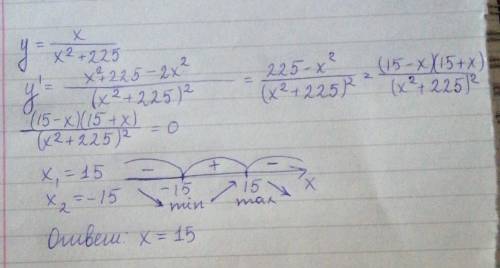
тогда (х+4) км в час - скорость катера по течению,
(х-4) км в час - скорость катера против течения.
12/(х+4) час.- время по течению;
4/(х-4) час. - время против течения.
Всего катер затратил 2 часа.
Составляем уравнение:
(12/(х+4)) + (4/(х-4))=2;
так как х≠-4 и х≠4 ( иначе катер не сможет плыть против течения)
умножаем на (х+4)(х-4)≠0
12(х-4) + 4(х+4) =2(х-4)(х+4);
12х-48 +4х+16=2х²-32;
х²-8х=0
х(х-8)=0
х=0 или х=8
х=0 не удовлетворяет условию задачи.
О т в е т. 8 км в час - собственная скорость катера.