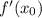производная функции в данной точке. А 
точка касания по иксу.
мы должны найти производную общего типа этой функции.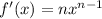
- где n это степень.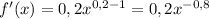
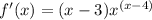
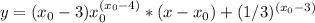
и получаешь уравнение касательной.
Дана функция y(x)= –2·x–3.
1) y(1)= –2·1–3= –2–3= –5; y(–1)= –2·(–1)–3= 2–3= –1;
y(0)= –2·0–3= 0–3= –3; y(–1/2)= –2·(–1/2)–3= 1–3= –2;
2) Определим значения x, при которых y(x)=1:
–2·x–3=1 ⇔ –2·x= 1+3 ⇔ –2·x= 4 ⇔ x= –2;
Определим значения x, при которых y(x)= –1:
–2·x–3= –1 ⇔ –2·x= –1+3 ⇔ –2·x= 2 ⇔ x= –1;
Определим значения x, при которых y(x)=0:
–2·x–3=0 ⇔ –2·x= 3 ⇔ x= –3/2;
3) Определим значения x, при которых функция принимает отрицательные значения, то есть решаем неравенство y(x)<0:
–2·x–3<0 ⇔ –3 < 2·x ⇔ –3/2 < x ⇔ x∈(–3/2; +∞).
20х15 = 300 м2 = 3000000см2 - площадь пола
20х20= 400см2 - площадь плитки (1шт)
3000000/400= 7500 плиток
x - в первую палатку
y - во 2 палатку
z - в 3 палатку
получаем: x+y=400 y+z=300 x+z=440
вычтем из 2ого третье уравнение: y-x = -140 x = y+140
подставим в 1ое уравнение: y+140+y=400
2y=260
y=130
во вторую палатку привезли 130кг