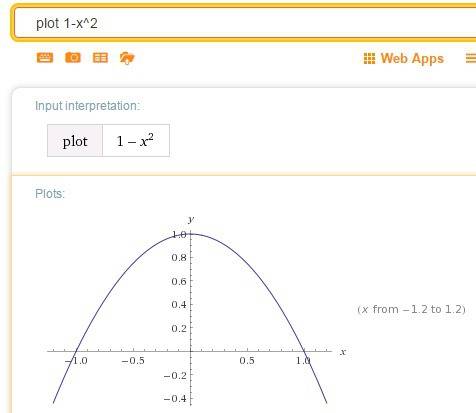
стоит минус
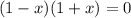
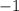и 
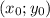- она же точка пересечения данной функции с осью ОУ: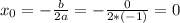
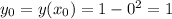
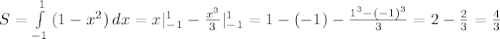
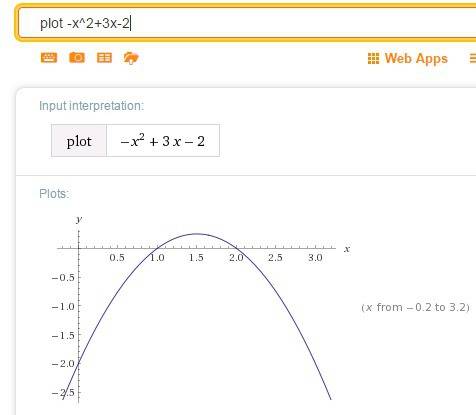
стоит минус
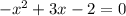
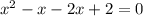
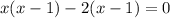
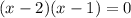
и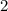 
:
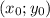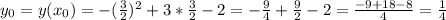
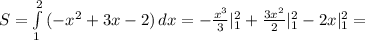
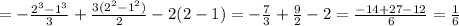
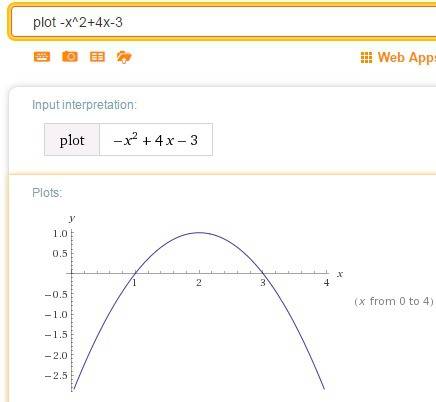
стоит минус
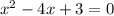
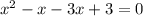
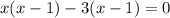
и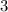 
:
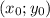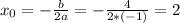
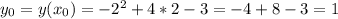
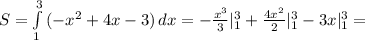
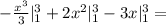
S = a · b = 13 · 13 = 169 см² - площадь ткани
| 5 cм | 5 см | 3 см |
⇵ ⇵ ⇵ ⇵ 13 · 1 см
5 см · 2 · 1 см · 13 = 130 см² (26 отрезов 5×1 см)
Остаётся 3 см по длине и 13 см по ширине
5 см · 2 (по ширине) · 1 см · 3 (по длине) = 30 см² (6 отрезов 5×1 см)
Остаётся 3 см по длине и 3 см по ширине = 9 см² (3×3 см - остаток)
Итого: 130 см² + 30 см² + 9 см² = 169 см² - площадь (по условию)
26 отрезов + 6 отрезов = 32 отреза размером 5×1 см и 9 см² - остаток
Вiдповiдь: 32 шматка (max).
