0,75
Объяснение:
Для решения применим правило нахождения геометрической вероятности: Если фигура F₁ содержится в фигуре F, тогда вероятность попадания в фигуру F₁, при условии попадания в фигуру F равна отношению площадей: Р=S(F₁):S(F)
Фигура первая - большой круг с радиусом 2 см, площадь которого равна πR² = π*2²=4π (см²)
Фигура вторая - маленький круг с радиусом 1 см, площадь которого равна πr² =π*1² =π (см²)
Событие А - "точка В попадет в маленький круг радиуса 1 см, находящийся внутри большого круга радиусом 2 см".
По правилу нахождения геометрической вероятности получаем вероятность попадания точки В в маленький круг радиуса 1 см:
Р(А) = π:4π = 1/4=0,25
Вероятность того, что точка В не попадёт в маленький круг радиуса 1 см, находящийся внутри большого круга радиуса 2 см, равна вероятности противоположного события событию А, т.е.
Р = 1-Р(А) = 1-0,25 = 0,75
*** Для решения использованы формула площади круга с радиусом R:
Sкр. = πR²
97,5
Объяснение:
Данная задача решаема через систему уравнения:
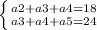
Решим эту систему при метода вычитания:
a3+a4=18-a2
a3+a4+24-a5
24-a5=18-a2
6-a5+a2=0
a5-a2=6 - данное выражение показывает нам разницу между членами прогресcии через a3 и a4
Разница между ближайшими членами d = 1,5 ,потому-что согласно a5-a2=6
Теперь есть формула:
a2=a1+d => d=1,5 => a2=a1+d ,тогда подставим в первое уравнение системы:
a1+1,5+a3+a4=18
Но при этом а3=a1+3 и а4=а1+4,5
Тогда:
a1+1,5+a1+3+а1+4,5=18
3*a1+9=18
a1=3
Находим все члены и их сумма равна:
3+4,5+6+7,5+9+10,5+12+13,5+15+16,5=97,5
ответ: 97,5
(В решении или в вычислениях могу ошибаться!)
стоимость установки счетчика составляет 3100, тогда
6*600=3600- экономия за 6 месяцев, больше чем 3100,
ответ: 6