Вероятность сдачи в срок всех экзаменов студентом факультета равна 0,7. с неравенства чебышева оценить вероятность того, что доля сдавших в срок все экзамены из 2000 студентов заключена в границах от 0,66 до 0,74.
2*4^x-3*10^x=5*25^xРазделим правую и левую части на 25^x. Получим 4^x 10^x2 - 3 = 5 25^x 25^x Так как степени у числетелей и знаменателей одинаковые можно поступить следующим образом 2* (4 : 25)^х - 3*(10 : 25)^х = 5Во второй дроби можно сократить 10 и 25 на 5. Получаем 2* (4 : 25)^х - 3*(2 : 5)^х = 5 Так как 4 = 2^2, a 25 = 5^2, получим следующее 2* (2 : 5)^2х - 3*(2 : 5)^х = 5 Введем новую переменную t = (2 : 5)^хПолучим новое уравнение2*t^2 - 3*t = 52*t^2 - 3*t - 5 = 0Решаем через дискриминант. a = 2, b = -3, c = -5D = b^2 -4ac = 9 - 4*2*(-5) = 9 + 40 = 49t(1) = (3 - 7) : 4 = -1t(2) = (3 + 7) : 4 = 2,5 x = -1 нам не подходит, так как ни при каких х (2 : 5)^х не будет отрицательным.Тогда получаем (2 : 5)^х = t(2) (2 : 5)^х = 5 : 2 (2 : 5)^х = (2 : 5)^(-1) х = -1 ответ: х = -1
Четырёхзначное число "abcd" можно представить в виде: а*1000+b*100+c*10+d, при этом произведение а*b*c*d =10, соответственно данное число может состоять из цифр 1,1,2 и 5. Очевидно, что делимое при делении без остатка на 28 (кратное 28) может заканчиваться только на 2, т.к. произведение 8 с другими числами не может образовывать в разряде единиц ни 1, ни 5. Остается три варианта четырёхзначных чисел это 1152, 1512 и 5112, из которых на 28 делится только 1512 (это 54). 1512 - это единственный ответ.
X — студент сдал в срок все экзамены.
Вероятность наступления события X равна p=0,7, тогда вероятность ненаступления события Х равна q = 1- p = 0.3
Случае n = 2000 испытаний, математическое ожидание:
а дисперсия:
Воспользуемся неравенством Чебышева:
где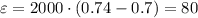
ответ: P ≥ 0.9344