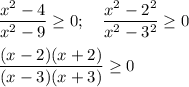
Решим неравенство методом интервалов.
Отмечаем на координатной прямой точки, в которых знаменатель и числитель обращаются в ноль. И выкалываем те, что из знаменателя. Мы получили 5 интервала. Перед дробью знак положительный и все множители имею пол. знак при х, поэтому на правом интервале ставим "плюс", далее чередуем знак через каждую отмеченную точку (все множители в нч степени - 1). Нас интересует, когда больше или равно, поэтому выбираем интервалы с плюсом, учитывая границы.
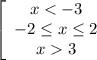
ответ: x ∈ (-∞;-3) ∪ [-2;2] ∪ (3;+∞).
В решении использовалась формула сокращённого умножения: a²-b²=(a-b)(a+b).

Сначала то, что попроще:
0 раз: вероятность (1-0,8)*(1-0,7)*(1-0,6)=0,024
3 раза: вероятность 0,8*0,7*0,6=0,336
Теперь, например, посчитаем вероятность того, что попали ровно 1 раз, т.е. попал один из них, а все остальные промахнулись:
0,8*(1-0,7)(1-0,6) + 0,7*(1-0,8)(1-0,6) + 0,6*(1-0,8)(1-0,7)=0,188
Последнюю вероятность (того, что попали ровно 2 раза) можно посчитать точно также, а можно просто воспользоваться тем, что сумма вероятностей должна быть равной единице
1-0,336-0,024-0,188=0,452
0,8*0,7*(1-0,6)+0,8*(1-0,7)*0,6+(1-0,8)*0,7*0,6=0,452
Если a=(-1 1/8), b=(-1 1/2), то (3*(-1 1/8) - 2*(-1 1/2))(2*(-1 1/8) + (-1 1/2)^2) = (3.375 - 3)(-2.25+2.25) = 0