ответ:53 липы 107 берез.
Объяснение: из условий ясно что рядом со всеми липами одинаковые деревья(либо две липы либо две берёзы) и только рядом с одной березой одинаковые деревья. Перебирая все варианты понимаем что условия выполнимы только если сажать деревья так. Л-липа Б- береза. >БЛББЛББЛББЛБББЛББЛББЛБ
Можно заметить в одном три берёзы подряд. Итого если продолжить эту цепочку до 160ти деревьев получим 53 группы БЛБ и одну одинокую березу между БЛБББЛБ . ВСЕ условия выполнены. Рядом с одной березой два одинаковых дерева (две берёзы) а рядом со всеми липами разные деревья (береза и липа).
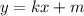 : если k>0, функция возрастает, k<0 - убывает. Всё просто. Т.е. в убывании обе функции линейные, k<0 и в первом (k=-7), и во втором
: если k>0, функция возрастает, k<0 - убывает. Всё просто. Т.е. в убывании обе функции линейные, k<0 и в первом (k=-7), и во втором 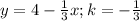 . С этим разобрались. Теперь к возрастанию. Я не знаю, в каком Вы классе, постараюсь объяснить доступно. Чтобы определить возрастание/убывание функции, нужно взять значения
. С этим разобрались. Теперь к возрастанию. Я не знаю, в каком Вы классе, постараюсь объяснить доступно. Чтобы определить возрастание/убывание функции, нужно взять значения 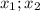 , два произвольных числа, но
, два произвольных числа, но 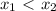 . Пусть мы имеем функцию
. Пусть мы имеем функцию  , тогда вычисляем значения функции в этих двух точках, имеем
, тогда вычисляем значения функции в этих двух точках, имеем 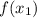 и
и 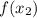 , так вот, если
, так вот, если  , тогда функция возрастающая, если же
, тогда функция возрастающая, если же 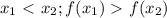 , то она убывающая, но только ПРИ УСЛОВИИ, что она монотонна на всей области определения (т.е. ТОЛЬКО возрастает или ТОЛЬКО убывает), в противном случае мы говорим о ПРОМЕЖУТКАХ возрастания и убывания. 1)
, то она убывающая, но только ПРИ УСЛОВИИ, что она монотонна на всей области определения (т.е. ТОЛЬКО возрастает или ТОЛЬКО убывает), в противном случае мы говорим о ПРОМЕЖУТКАХ возрастания и убывания. 1)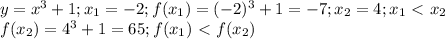 , т.е. функция возрастающая. А вот задание с
, т.е. функция возрастающая. А вот задание с 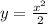 не совсем корректно, так как эта функция возрастает только при x>0, при x<0 она убывает, x=0 - Точка экстремума. Если уж брать математический анализ, то легко взять производную и исследовать функцию на "скорость изменения" (алгебраический смысл производной)
не совсем корректно, так как эта функция возрастает только при x>0, при x<0 она убывает, x=0 - Точка экстремума. Если уж брать математический анализ, то легко взять производную и исследовать функцию на "скорость изменения" (алгебраический смысл производной) 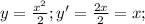 . Если производная в некоторой точке отрицательная, то функция убывает, если производная положительная, то функция возрастает, если производная равна 0, то это точка экстремума. Очевидно, что при x<0 функция убывает, при x>0 возрастает. Если же доказывать возрастание на промежутке x>0, тогда действуем, как и в первом случае (только не берем значения из ненужного нам промежутка):
. Если производная в некоторой точке отрицательная, то функция убывает, если производная положительная, то функция возрастает, если производная равна 0, то это точка экстремума. Очевидно, что при x<0 функция убывает, при x>0 возрастает. Если же доказывать возрастание на промежутке x>0, тогда действуем, как и в первом случае (только не берем значения из ненужного нам промежутка): 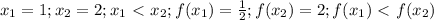 , функция возрастает, что и требовалось доказать.
, функция возрастает, что и требовалось доказать.
ответ: 1