Впрогрессии с положительными членами s2=4, s3=13. найти s5

👇

Ответ:

soos4

29.05.2021

$\\a_3=S_3-S_2, \ a_n0 \ \wedge \ q1
\\
\\a_3=13-4=9
\\
\\a_1+a_2=4
\\
\\\begin{cases}a_1*q^2=9\implies a_1=\frac{9}{q^2}\\a_1+a_1q=4\end{cases}
\\
\\\frac{9}{q^2}+\frac 9q=4/*q^2
\\
\\4q^2-9q-9=0
\\
\\\Delta=9^2+4*4*9=81+144=225
$

$\\q=\frac18(9-15)=-\frac34\notin D, \ q=\frac18(9+15)=3
\\
\\a_1=\frac{9}{3^2}=1
\\
\\S_n=a_1*\frac{1-q^n}{1-q}
\\
\\S_5=\frac{1-3^5}{1-3}=\frac12(243-1)=121$

4,6(83 оценок)

Ответ:

ilka2004z

29.05.2021

Если члены прогрессии положительны, то она имеет вид
1; 3; 9; 27; 81...
Сумма первых пяти членов равна 1 + 3 + 9 + 27 + 81 = 121

По формуле суммы первых двух членов прогрессии:
b1(1-q^2)/(1-q) = 4, откуда b1(1+q) = 4, или b1 = 4/(1+q)
По формуле суммы первых трех членов прогрессии:
b1(1-q)(1+q+q^2) = 13(1-q), откуда b1(1+q+q^2) = 13.
Выполняем подстановку:
4(1+q+q^2) /(1+q)= 13, откуда q = 3 (отрицательное значение знаменателя отбрасываем, так как нас интересуют только положительные члены)
b1 = 4/(1+3) = 1

Итак, первый член прогрессии равне 1, знаменатель прогрессии равен 3.
S5 = 1(1 - 3^5)/(1-3) = 121

ответ: 121

4,8(12 оценок)

Открыть все ответы

Ответ:

tarasIT

29.05.2021

Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f(x) > 0. Алгоритм состоит из 5 шагов:

Решить уравнение f(x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;

Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;

Найти кратность корней. Если корни четной кратности, то над корнем рисуем петлю. (Корень считается кратным, если существует четное количество одинаковых решений)

Выяснить знак (плюс или минус) функции f(x) на самом правом интервале. Для этого достаточно подставить в f(x) любое число, которое будет правее всех отмеченных корней;

Отметить знаки на остальных интервалах, чередуя их.

После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f(x) > 0, или знаком «−», если неравенство имеет вид f(x) < 0.

В случае с нестрогими неравенствами( ≤ , ≥) необходимо включить в интервалы точки, которые являются решением уравнения f(x) = 0;

Решить неравенство:

(x - 2)(x + 7) < 0

Работаем по методу интервалов.

Шаг 1: заменяем неравенство уравнением и решаем его:

(x - 2)(x + 7) = 0

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:

x - 2 = 0 => x = 2

x + 7 = 0 => x = -7

Получили два корня.

Шаг 2: отмечаем эти корни на координатной прямой. Имеем:

Шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000).

Получим:

f(x) = (x - 2)(x + 7)

x = 3

f(3)=(3 - 2)(3 + 7) = 1*10 = 10

Получаем, что f(3) = 10 > 0 (10 – это положительное число), поэтому в самом правом интервале ставим знак плюс.

Шаг 4: нужно отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус. Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси.

Вернемся к исходному неравенству, которое имело вид:

(x - 2)(x + 7) < 0

Итак, функция должна быть меньше нуля. Значит, нас интересует знак минус, который возникает лишь на одном интервале: (−7; 2). Это и будет ответ.

Пример 2:

Решить неравенство:

(9x2 - 6x + 1)(x - 2) ≥ 0

Решение:

Для начала необходимо найти корни уравнения

(9x2 - 6x + 1)(x - 2) = 0

Свернем первую скобку, получим:

(3x - 1)2(x - 2) = 0

Отсюда:

x - 2 = 0; (3x - 1)2 = 0

Решив эти уравнения получим:

x1 = 2; x2 = ; x3= ;

Нанесем точки на числовую прямую:

Т.к. x2 и x3 – кратные корни, то на прямой будет одна точка и над ней “петля”.

Возьмем любое число меньшее самой левой точки и подставим в исходное неравенство. Возьмем число -1.

(9*(-1)2 - 6*(-1) + 1)(-1 - 2) = -12

Т.к. решение уравнения при x = -1 отрицательное (-12), то на графике в крайнем левом интервале пишем -, и далее чередуя знак записываем его в следующие интервалы:

Далее выбираем отрицательные интервалы, т.к. знак нашего неравенства ≤.

Не забываем включать решение уравнения (найденные X), т.к. наше неравенство нестрогое.

ответ: {} U [2;+∞)

Пример 3:

Решить неравенство:

(9x2 - 6x + 1)(x - 2) > 0

Все, чем данное неравенство отличается от предыдущего – вместо нестрогого неравенства (≥) стоит строгое (>). Как ни странно, решение данного неравенства будет иным.

Найдем корни уравнения (9x2 - 6x + 1)(x - 2) ≠ 0 (знак ≠ означает, что найденные корни не могут быть решениями нашего неравенства, т.к. оно строгое). Проделав все этапы, что и в предыдущем примере получим:

x1= 2; x2,3 =;

Вынесем наши решения на числовую прямую (обратите внимания, что данные точки не включены, т.к. неравенство строгое, т.е. левая часть неравенства не равна нулю)

Обратите внимание, что корни x2 и x3 совпадают, корень “” является кратным. Соответственно, в данной точке на числовой прямой рисуем петлю.

Возьмем число -1.

(9*(-1)2 - 6*(-1) + 1)(-1 - 2) = -12

Т.к. решение уравнения при x = -1 отрицательное (-12), то на графике в крайнем левом интервале пишем -, и далее чередуя знак записываем его в следующие интервалы:

Далее выбираем отрицательные интервалы, т.к. знак нашего неравенства <.

Найденные корни не включаем в ответ.

ответ: (2;+∞).

4,4(47 оценок)

Ответ:

Vladiko011

29.05.2021

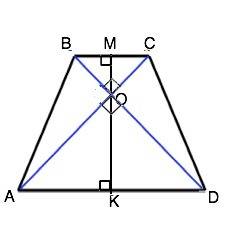
Диагонали равнобедренной трапеции равны и при пересечении образуют с её основаниями равнобедренные треугольники, а так как диагонали данной трапеции взаимно перпендикулярны, эти треугольники - прямоугольные. ОМ и ОК - медианы и высоты равнобедренных треугольников, перпендикулярны параллельным основаниям и проходят через одну точку О, следовательно, лежат на одной прямой. Отрезок МК, который соединяет середины оснований трапеции, - сумма медиан этих треугольников.

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине ⇒ МО=ВС:2, ОК=АD:2, ⇒ ВМ+АК=МК. Но ВМ+АК = полусумма оснований, т.е. равна средней линии трапеции. Следовательно, средняя линия трапеции АВСD равна МК и равна 0,8