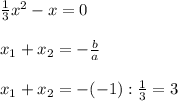
Раз оба корня равны нули, значит они равные. А равные корни могут быть только при дискриминанте D=0.
D=b^2-4ac a=1,b=-a^2-3a,c=3a-a^2 D=0
(-a^2-3a)^2-4(3a-a^2)=0
(a^2+3a)^2-4(3a-a^2)=0
Так и оставляем дискиминант.
x1=(-b-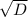 )/2a.
)/2a.
x2=(-b+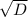 )/2a.
)/2a.
x1=x2=0, D=0
-b/2a=0
-(-a^2-3a)/2=0
a^2+3a=0
a(a+3)=0
a=0 или a=-3.
Теперь проверяем, удолетворяет ли найденные нами a решению уравнения с параметром. Для этого подставим их в уравнение дискриминанта:
(a^2+3a)^2-4(3a-a^2)=0
(0+0)^2-4(0-0)=0
0=0
a=0 - удолетворяет
(9-9)^2-4(-9-9)=0
72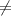 0
0
a=-3 - не удолетворяет условию.
ответ: 0.
Пусть первая принесла x кг яблок a вторая получается - 210-x
y - цена яблок первой женщины
z - цена яблок второго.
Мы знаем что они получили одинаковое количество денег тоесть yx=(210-x)z. Выразим отсюда 210-x=yx/z
Из утверждения: "Если бы первая продала столько же яблок,сколько и вторая,то она получила бы n рублей" получаем: y(210-x)=n
а из: "если бы вторая продала столько же яблок,сколько первая,то она получила бы 4n рублей." получаем: xz=4n. Подставим сюда вместо n y(210-x) получим:
xz=4y(210-x).Подставим вместо (210-x) выражение yx/z.Получим что:
xz=4y^2x/z => z^2=4y^2 => z=2y. То есть второая женщина продовала яблоки 2 раза дороже.Теперь подставим z=2y в yx=(210-x)z Получим что x=420-2x =>3x=420 => x=140. Тоесть у первой было 140 кг яблок значит у второй 210-140 => 70кг.