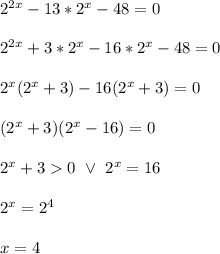
катер плыл сначала 30 минут против течения реки, а затем 15 минут по озеру в отсутствии течения. найдите скорость течения реки(км/ч).если собственная скорость катера постоянна и равна 20 км/час, а средняя скорость его движения за весь промежуток времени составила 17 км
x - скорость течения реки
0,5 (20-x ) - путь, пройденный катером против течения реки,
0,25·20=5 - путь, пройденный катером по озеру
(0,5+0,25) - время, которое катер был в пути.
(0,5 (20-x ) + 5)/ (0,5+0,25) = 17 - средняя скорость катера
(10-0,5x+5)/(0,75)=17
(15-0,5x)=17·3/4
60-2x=51 x=9/2 x=4,5
Возьмём скорость пропускания второй трубы за х, тогда скорость пропускания первой=х-4
Время, за которое первая труба заполняет 672л воды=672/х-4, а время, за которое 2 труба заполняет 560л воды=560/х. Известно что 2 труба заполняет свой резервуар на 8 минут быстрее, поэтому можно составить уравнение:
672/(х-4) - 560/х=8 домножаем всё на х(х-4) сразу укажем что х не может быть равен 4 (тк при этом идёт деление на ноль чего делать нельзя)
получаем:
672х-560(х-4)=8х(х-4)
672х-560х+2240=8х^2-32х переносим всё в правую часть и считаем
8х^2-144х-2240=0 разделим всё на 8
х^2-18х-280=0
D=18*18+4*280=324+1120=38^2
отсюда х1=(18-38)/2=-10(пост корень тк скор пропускания не может быть отриц)
х2=18+38/2=28
Значит 1 труба пропускает 28-4=24л воды а вторая-28л воды
у²-13у-48=0
по т.Виета
у₁+у₂=13
у₁ * у₂ =-48
у₁=16 у₂= -3 ∉ по ОДЗ
2 в степени х=16 ⇒ х=4