В решении.
Объяснение:
Одночлен, у которого единственный числовой множитель стоит на первом месте и буквенные множители в различных степенях не повторяются, называется одночленом стандартного вида.
Числовой сомножитель называют коэффициентом одночлена.
Степенью одночлена называют сумму показателей всех переменных входящих в этот одночлен.
Одночлен Станд.вид Коэффиц. Степень
1,2с⁴с⁸ 1,2с¹² 1,2 12
0,6m²n³*4m⁵n² 2,4m⁷n⁵ 2,4 7+5=12
2/7a²*3,5b a²b 1 2+1=3
-5x²*0,2xy -x³y -1 3+1=4
-1,6x³y⁶*0,5x²y⁵ -0,8x⁵y¹¹ -0,8 5+11=16
a ∈ ∅
Объяснение:
Графиком трехчлена в левой части является парабола. В таком случае, условие "меньше 0" означает, что график лежит целиком под осью абсцисс, а ветви параболы направлены вниз ( a<0 ).
Если график лежит целиком под осью абсцисс, то нет пересечения графика с осью x, что равносильно отсутствию действительных корней квадратного трехчлена (дискриминант меньше 0).
Т.к. ветви параболы направлены вниз, то параметр a можно представить в виде:
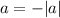
Тогда дискриминант равен:
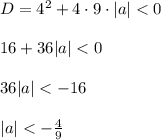
Получили противоречие (модуль не может быть отрицательным).
Значит не существует такого параметра a, при котором неравенство будет верно при любых значениях x
y`=-2x-8=-2(x+4)=0
x=-4
y(-4)=-16+32+11=27