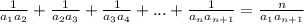
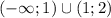
Объяснение:
Перенесём один из корней влево, а одну из семёрок — вправо следующим образом:
![7^{ax^2-2x}-7^{x^2-1}=\sqrt[7]{2x-ax^2}-\sqrt[7]{1-x^2} \\7^{ax^2-2x}-\sqrt[7]{2x-ax^2}=7^{x^2-1}-\sqrt[7]{1-x^2}\\7^{ax^2-2x}+\sqrt[7]{ax^2-2x} =7^{x^2-1}+\sqrt[7]{x^2-1}](/tpl/images/4771/4253/b4ecf.png)
Рассмотрим функцию ![f(x)=7^x+\sqrt[7]{x}](/tpl/images/4771/4253/5e929.png) . Она представляет собой сумму двух монотонно возрастающих функций (показательная и функция корня седьмой степени), следовательно она также монотонно возрастает. Значит, каждому аргументу соответствует ровно одно значение функции, то есть функция f(x) взаимно однозначна.
. Она представляет собой сумму двух монотонно возрастающих функций (показательная и функция корня седьмой степени), следовательно она также монотонно возрастает. Значит, каждому аргументу соответствует ровно одно значение функции, то есть функция f(x) взаимно однозначна.
Уравнение в таком случае принимает следующий вид:
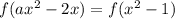
Поскольку каждому значению функции соответствует только одно значение аргумента, равенство значений функции можно свести к равенству её аргументов:
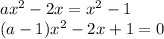
Если 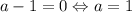 , то это линейное уравнение, имеющее не более одного корня, что не подходит.
, то это линейное уравнение, имеющее не более одного корня, что не подходит.
Если 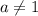 , то это квадратное уравнение. Оно имеет два корня при положительном дискриминанте:
, то это квадратное уравнение. Оно имеет два корня при положительном дискриминанте:
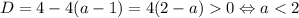
Учитывая, что 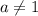 , получаем ответ
, получаем ответ 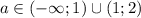
а) - 2 ответа
б) - нет ответов
в) - 2 ответа
г) - 2 ответа
Объяснение:
а) х⁴ - 81 = 0
Перенос :
х⁴ = 81
81 = 3^4
х⁴ = 3^4
x = -3 или 3
б) х⁴ + 169 = 0
Перенос :
х⁴ = -169 => Уравнение не имеет значений, так как степень числа не может быть отрицательным числом.
в) 25х⁴ - 49 = 0
Перенос :
25х⁴ = 49
49 = 7^2
25х⁴ = (5x^2)^2
25х⁴ = 7^2
5x^2 = 7
x^2 = 1,4
г) 6х⁴ - 144 = 0
144 = 12^2
16 = 4^2
(4x^2)^2 = 12^2
4x^2 = 12
x^2 = 3
Если моё решение оказалось верным, я бы хотел Вас попросить отметить мой ответ как лучший, а так же оставить отзыв о качестве моей работы (каким бы он ни был). Рад был оказать Вам
Тогда
3s=3/1*4 +3/4*7+3/(3n-2)(3n+1)
Разложим каждое слагаемое в виде разности дробей:
3s=(1-1/4)+(1/4-1/7)+(1/7-1/10)+(1/(3n-2) -1/(3n+1))
все дроби кроме первого и последнего попарно уничтожаются.
Откуда
3s=1-1/(3n+1)=3n/(3n+1)
S=n/(3n+1)
Тк нам нужно найти наименьшее n ,то естественно рассмотрим случай когда сумма меньше чем 1/3,тк естественно в этом случае n будет наименьшим,ведь при возрастании n сумма возрастает.
Тогда верно неравенство:
1/3-n/(3n+1)<1/1000
1-3n/3n+1<3/1000
1- (3n+1-1)/(3n+1)<3/1000
1-(1- 1/3n+1)<3/1000
1/(3n+1)<3/1000
Очевидно что при возрастании n левая часть убывает,поэтому тк нас интересуют только натуральные n,то верно что
3n+1>1000/3
9n+3>1000
9n>997
n>997/9=110 +7/9, А тк n-число натуральное то
Очевидно что наименьшее натуральное n=111
ответ:111