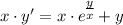
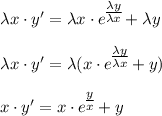
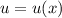 с замены:
с замены: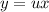 , тогда
, тогда 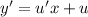
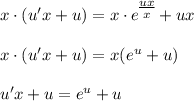
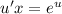
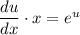 - уравнение с разделяющимися переменными.
- уравнение с разделяющимися переменными.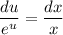 - уравнение с разделёнными переменными.
- уравнение с разделёнными переменными.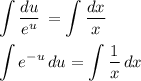
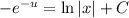 - общий интеграл новой функции.
- общий интеграл новой функции. из решения уравнения с разделяющимися переменными, чтобы записать решение исходного однородного уравнения, остаётся выполнить обратную замену:
из решения уравнения с разделяющимися переменными, чтобы записать решение исходного однородного уравнения, остаётся выполнить обратную замену: 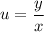
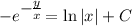 - общий интеграл исходного уравнения.
- общий интеграл исходного уравнения.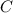 . Подставим в общий интеграл начальное условие:
. Подставим в общий интеграл начальное условие: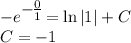
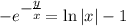 - частный интеграл, также является решением данного дифференциального уравнения.
- частный интеграл, также является решением данного дифференциального уравнения.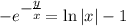
Т.к. точка (0.0) ей принадлежит, то b = 0, осталось найти k. Подставляем координаты второй точки, получаем -3 = 12k, откуда k = -1\4
y = -x\4 - искомая функция
2.Параллельность означает одинаковый коэффициент наклона, т.е. число перед х. k = -6.
Подставляем точку, получаем -10 = 1*(-6) + b, откуда b = -4
y = -6x - 4