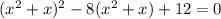
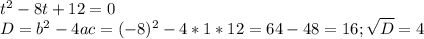
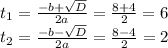
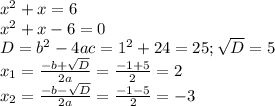
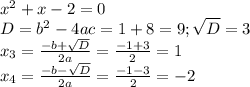
y=1+x3, х∈(-∞;+∞) или D=(-∞;+∞)
y=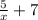 , х∈(-∞;0)∪(0;+∞) или D=(-∞;0)∪(0;+∞)
, х∈(-∞;0)∪(0;+∞) или D=(-∞;0)∪(0;+∞)
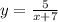 , х∈(-∞;-7)∪(-7;+∞) или D=(-∞;-7)∪(-7;+∞)
, х∈(-∞;-7)∪(-7;+∞) или D=(-∞;-7)∪(-7;+∞)
Объяснение:
Область определения функции - откуда до куда твой график существует по оси Х.
а) y=1+x3 график прямой х∈(-∞;+∞)
б) y=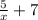 график гиберболы х∈(-∞;0)∪(0;+∞)
график гиберболы х∈(-∞;0)∪(0;+∞)
Если функция имеет вид: 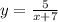 то х∈(-∞;-7)∪(-7;+∞)
то х∈(-∞;-7)∪(-7;+∞)
Знаменатель х+7 говорит о том, что асимптота сдвинута по оси х влево.
Можно записывать ответ по разному, два варианта записи ответа, необходимо выбрать 1:
y=1+x3, (1вариант) х∈(-∞;+∞) или (2 вариант) D=(-∞;+∞)
y=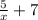 , (1вариант) х∈(-∞;0)∪(0;+∞) или (2 вариант) D=(-∞;0)∪(0;+∞)
, (1вариант) х∈(-∞;0)∪(0;+∞) или (2 вариант) D=(-∞;0)∪(0;+∞)
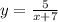 , (1вариант) х∈(-∞;-7)∪(-7;+∞) или (2 вариант) D=(-∞;-7)∪(-7;+∞)
, (1вариант) х∈(-∞;-7)∪(-7;+∞) или (2 вариант) D=(-∞;-7)∪(-7;+∞)
Точки с координатами (-2;8) и (1;5)
Объяснение:
Первая функция
у= х²+4 (1)
Выразим у во второй функции:
х+у = 6 <=> у = 6-х (2)
Точка пересечения - точка, с некими координатами (х0;у0), которые принадлежат обоим графикам функций.
То есть нам надо найти такие х и у, для которых верно равенство 1 и 2.
Приравняем у в (1) и (2) функциях. Получим:
у = х²+4 = 6-х
Или

Найдем у для х=(-2) и х=1
Для этого подставим значение х в любую из 2х функций
При х = (-2)
у(-2) = 6-(-2) = 6+2 = 8
Следовательно одна из искомых точек имеет координаты:
(-2;8)
При х=1
у(1) = 6-1 = 5
Следовательно вьорая искомая точек имеет координаты:
(1;5)
ответ: (-2;8) и (1;5)
(х² + х)=а
а²-8а+12=0
а1=2
а2=6
х² + х=2
х² + х-2=0⇒х=-2 или х=1
х² + х=6
х² + х-6=0⇒ х=-3 или х=2