
Объяснение:

В знаменателе с точностью до какого-то коэффициента u должен стоять косинус суммы:

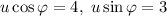
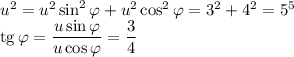
u можно взять положительным, тогда u = 5; 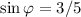 ,
,  . Можно было бы взять и отрицательным, при этом были бы другие знаки у синуса и косинуса.
. Можно было бы взять и отрицательным, при этом были бы другие знаки у синуса и косинуса.
φ тоже можно взять любым, лишь бы у синуса и косинуса были нужные знаки (если u > 0, и то и то будет положительным) и тангенс был равен найденному значению. Я возьму  , это угол первой четверти.
, это угол первой четверти.
В числителе должно стоять
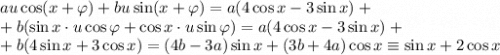
Приравниваем коэффициенты и решаем получившуюся систему:
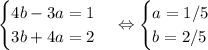
1) 1-3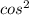 x=2sin(x)cos(x)
x=2sin(x)cos(x)
единицу представим по тригонометрическому тождеству:1=sin²x+cos²x
sin²x+cos²x-3cos²x-2sin(x)cos(x)=0
sin²x-2sin(x)cos(x)-2cos²x=0
делим каждый член уравнения на cos²x
tg²x-2tgx-2=0
решаем квадратное уравнение
D=12
tgx₁=1+√3 tgx₂=1-√3
x₁=arctg(1+√3)+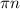 x₂=arctg(1-√3)+
x₂=arctg(1-√3)+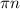
2) 3Sin²x+2SinxCosx=2
3Sin²x+2SinxCosx=2(Sin²x+Cos²x)
Sin²x+2SinxCosx-2Cos²x=0
Уравнение однородное 2 степени. Разделим его на Cos²x
Tg²x+2Tgx-2=0
Tgx=y
y²+2y-2=0
D=12>0
y=(-2+2√3)/2=-1+√3 или y=(-2-2√3)/2= -1-√3
Tgx=-1+√3⇒ x=arctg(-1+√3)+πn,n∈Z
Tgx= -1-√3 ⇒x= arctg(-1-√3)+πn,n∈Z
В первом сосуде было на 5 литров меньше, чем во втором всего раствора.
А не чистой кислоты.
Так как очень смущает вопрос , где нужно найти кислоту а не раствор.
Я нашла именно объем раствора в сосудах.
И в результате получилось, что он не зависит от концентрации кислот.
Пусть в первом сосуде было x литров раствора.
А концентрация была а (не процент, а коэффициент , что бы не мучатся с делением на 100). Значит чистой кислоты в нем было х*а литров.
Тогда после того как из него забрали 6 литров, в первом сосуде осталось (х-6) литров. А кислоты осталось (х-6)*а литров.
Пусть во втором концентрация была в.
Тогда после того как из второго сосуда налили 6 литров, в первом стало (х-6)*а+6*в литров кислоты.
Для нахождения концентрации необходимо объем кислоты разделить на весь объем раствора. Так как из первого взяли 6 литров и добавили 6 литров, значит в нем осталось х+6-6=х литров раствора.
Получаем окончательную концентрацию в первом сосуде
((х-6)*а+6*в)/х
Аналогично находим концентрацию во втором сосуде:
Объем раствора (х+5) литров
Объем кислоты в начале (х+5)*в литров
Объем кислоты после того как взяли 6 литров раствора
(х+5-6)*в=(х-1)*в литров
Объем кислоты после того как добавили 6 литров раствора из первого
(х-1)*в+6*а литров
Получаем окончательную концентрацию во втором сосуде
((х-1)*в+6*а)/(х+5)
Так как концентрации в первом и во втором сосуде равны
((х-6)*а+6*в)/х=((х-1)*в+6*а)/(х+5)
(ах-6а+6в)/х=(вх-в+6а)/(х+5)
Приводи к общему знаменателю х*(х+5)
Умножим левую часть на (х+5), а правую х
При условии, что х≠0 и х≠-5, Получаем:
ах²-6ах+6вх+5ах-30а+30в=вх²-вх+6ах
ах²-вх²-7ах+7вх-30а+30в=0
х²(а-в)-7х(а-в)-30(а-в)=0
Д=(-7(а-в))²+4*(а-в)*30(а-в)=49(а-в)²+120(а-в)²=169(а-в)²
√Д=√169(а-в)²=13(а-в)
х1=(7(а-в)-13(а-в))(2*(а-в))=-6(а-в)/2(а-в)=-3 Не подходит по условию
х2=(7(а-в)+13(а-в))(2*(а-в))=20(а-в)/2(а-в)=10
Значит в первом сосуде было -- 10 литров раствора кислоты
а во втором --- (х+5)=10+5=15 литров.
Если все таки нужно найти объем кислоты, а попутно проверить задачу.
Возьмем произвольно концентрацию для первого 10%=10/100=0,1, а второго 50%=50/100=0,5.
Тогда в первом было 10л*0,01=1 литр кислоты
Взяли 6л*0,1=0,6 литра, а налили 6*0,5=3 литра кислоты
Стало 1л-0,6л+3л=3,4 литра
Концентрация в Первом сосуде 3,4л/10л=0,34
Во втором было 15л*0,5=7,5 литра
Забрали 6л*0,5=3 литра, добавили 6л*0,1=0,6 литра.
Стало 7,5л-3л+0,6л=5,1 литра кислоты
Концентрация стала 5,1л/15л=3,4