1. Прежде найдем производную. она равна 12-3х², далее найдем критические точки. 12-3х²=0, х²=4; х=±2, установим с метода интервалов знаки производной при переходе через критич. точки.
-22
- + -
Точка х=-2 - точка минимума, т.к. при переходе через нее производная меняет знак с минуса на плюс, а точка х=2 - точка максимума, т.к. меняет производная знак с плюса на минус. Эти точки и есть точки экстремума.
2.Угол между диагональю и большей стороной равен 30°, поэтому меньшая сторона равна половине диагонали 12/2=6, это высота цилиндра -фигуры вращения прямоугольника вокруг меньшей стороны , а радиус его основания равен большей стороне 12*sin60° =12*√3/2=6√3
S=2πR(R+h)=2*π*6√3(6√3+6)=(216+72√3)π/см²/
Кол-во учащихся
"1" 0
"2" 5
"3" 3
"4" 0
"5" 2
"6" 11 - наибольшее кол-во учащихся
"7" 9
"8" 4
"9" 5
"10" 1
а)Объём выборки - общее кол-во учащихся:
0+5+3+0+2+11+9+4+5+1=40
b) , полученный наибольшим ко-вом учащихся равен "6"
с) Кол-во учащихся, получивших высокий : 5+4+1=10
Процент учащихся, получивших высокий :
(10/40)*100%=25%
ответ: 4, 8, 16Обозначим данные числа x, y и z; они образуют геометрическую прогрессию. Поусловию, числа x, y +2, z образуют арифметическую прогрессию, а числа x, y +2, z +9 — сновагеометрическую. Получаем систему уравнений:
y2 = xz,
2(y + 2) = x + z
(y + 2)2 = x(z + 9).
(первое и третье уравнения — характеризация геометрической прогрессии, второе уравнение —характеризация арифметической прогрессии).
Из первого и третьего уравнений получим 4y + 4 = 9x.
Выражая z из второго уравнения иподставляя в первое, получим y2 = 2xy+4x−x2.
Остаётся решить систему этих двух уравнений относительно x и y и затем найти z
ответ:4,8,16
Объяснение:
я не уверен то что это правильно но удачи
1) x=±2
2) 678,24+226,08√3≈1069,22
Пошаговое объяснение:
1) Точки экстремума - точки, в которых производная обращается в 0 и, проходя через которые, меняет свой знак.
Найдём производную: f'(x)=12-3x^2
Приравняем к 0: 12-3x^2=0
4-x^2=0
x^2-4=0
x=±2
Это и есть точки экстремумов функции
2) Фигура вращения прямоугольника вокруг стороны a с оставшейся стороной b - цилиндр с высотой a и радиусом b.
Чертёж прилагается. ∠ACD=60° => ∠CAD=30° => по свойству катета, лежащего против угла в 30°, CD=AC/2=12/2=6 => по теореме Пифагора AD=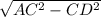 =
=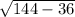 =6√3
=6√3
S=2πr(r+h)=2*3,14*6√3(6√3+6)=678,24+226,08√3≈1069,22