1. В прямоугольном треугольнике ABC угол А=55, угол С=90 длина одного из катетов 3см, гипотенузы 5см, а периметр равн 12см. Найдите угол В и второй катет.
2. Диагонали ромба АВСD пересекаются в точке О, УГОЛ BAD=40. Найдите углы треугольник АОВ
Объяснение:
1)ΔАВС, неизвестная сторона равна Р-3-5=12-8=4 (см).
По свойству острых углов прямоугольного треугольника
∠В=90°-55°=35°. Угол ∠В меньший острый угол, значит против него лежит меньшая сторона АС=3 см. Тогда ВС=4см.
2)По свойству диагоналей ромба ( делят углы пополам)∠ВАО=20°.
ΔАОВ-прямоугольный , по св. диагоналей ромба( взаимно-перпендикулярны) ∠АВО=90°-20°=70°.
Тогда ∠АВС=70°*2=140°
Углы ромба ∠ВАD=40°, ∠DСВ=40°( как противоположные углы), ∠АВС=140°, ∠АDС=140° ( как противоположные).
В обоих случаях рассматриваем прямоугольный треугольник с одним из углов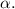 
В первом случае примем прилежащий к углу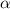 
катет за 3, а гипотенузу - за 5. Тогда неизвестный катет вычислим по т. Пифагора как 
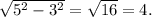Синус угла 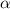есть отношение противолежащего катета к гипотенузе, т.е. 4/5. Тангенсом - отношение противолежащего катета к прилежащему, т.е. 4/3. Котангенсом - отношение прилежащего катета к противолежащему, т.е. 3/4.
Во втором случае примем катет, лежащий против 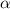за 4, а гипотенузу - за 5. Неизвестный катет, по теореме Пифагора, будет равен 3. Косинусом 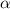есть отношение прилежащего катета к гипотенузе, т.е. 3/5. Тангенсом - отношение противолежащего катета к прилежащему, т.е. 4/3. Котангенсом - отношение прилежащего катета к противолежащему, т.е. 3/4.
