0,5+m
Объяснение:
Для того, чтобы найти требуемое значение логарифма log49(28), которого обозначим через L, воспользуемся следующей формулой loga(b / с) = logab / logaс (где а > 0, a ≠ 1, b > 0, c > 0), которая называется формулой перехода к новому основанию.
В нашем примере новым основанием будет число 7, так как дано log7(2) = m. Итак, имеем L = log7(28) / log7(49). Поскольку 28 = 7 * 22 и 49 = 72, то используя следующие формулы, преобразуем полученное выражение: loga(b * с) = logab + logaс (где а > 0, a ≠ 1, b > 0, c > 0) и logabn = n * logab (где а > 0, a ≠ 1, b > 0, n – любое число). Получим: L = log7(7 * 22) / log7(72) = (log7(7) + log7(22)) / log7(72) = (log7(7) + 2 * log7(2)) / (2 * log7(7)).
Очевидно, что log7(7) = 1. Тогда, имеем: L = (1 + 2 * m) / (2 * 1) = 1 : 2 + 2 * m : 2 = 0,5 + m.
Пусть в сектор  вписан прямоугольник
вписан прямоугольник 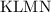 .
.  и
и  - середины сторон
- середины сторон  и
и  соответственно. Так как прямоугольник симметричен оси симметрии сектора, то две его стороны перпендикулярны этой оси, а две другие стороны - параллельны этой оси.
соответственно. Так как прямоугольник симметричен оси симметрии сектора, то две его стороны перпендикулярны этой оси, а две другие стороны - параллельны этой оси.
Так как прямоугольник симметричен оси симметрии сектора, то:
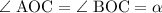
Проведем луч  , составляющий с осью симметрии сектора угол
, составляющий с осью симметрии сектора угол  . Зададим ограничения на х:
. Зададим ограничения на х: ![x\in[0;\ \alpha ]](/tpl/images/1361/0024/bc17d.png)
Найдем сторону прямоугольника, перпендикулярную оси симметрии сектора.
Рассмотрим треугольник  . Запишем соотношение для синуса угла х:
. Запишем соотношение для синуса угла х:
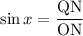
Заметим, что 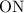 соответствует радиусу сектора. Тогда, выражение для
соответствует радиусу сектора. Тогда, выражение для 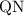 примет вид:
примет вид:

Так как 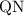 - половина стороны
- половина стороны  , то найдена первая сторона прямоугольника:
, то найдена первая сторона прямоугольника:

Найдем сторону прямоугольника, параллельную оси симметрии сектора. Представим ее длину в виде:
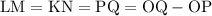
Длину найдем из того же прямоугольного треугольника  , записав выражение для косинуса угла
, записав выражение для косинуса угла  :
:

Выражаем  :
:
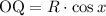
Длину  найдем из прямоугольного треугольника
найдем из прямоугольного треугольника 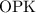 . Запишем выражение для тангенса угла
. Запишем выражение для тангенса угла  :
:

Откуда:

Так как 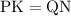 , то:
, то:
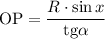
Таким образом, найдена вторая сторона прямоугольника:

Площадь прямоугольника равна произведению его смежных сторон:


Найдем производную:
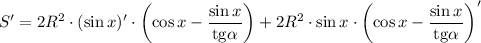

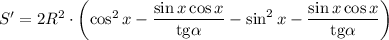
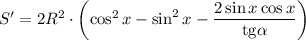
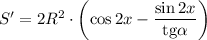
Приравняем производную к нулю:
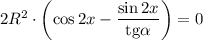
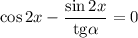
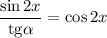
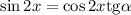
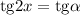
Учитывая ограничения ![x\in[0;\ \alpha ]](/tpl/images/1361/0024/bc17d.png) получим, что:
получим, что:
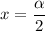
Проверим, является ли эта точка точкой экстремума.
Найдем значение производной при 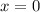 :
:

Найдем значение производной при  :
:
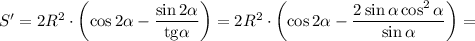
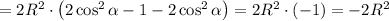
При переходе через точку 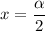 производная меняет знак с плюса на минус. Значит, это точка максимума.
производная меняет знак с плюса на минус. Значит, это точка максимума.
Найдем значение максимума:


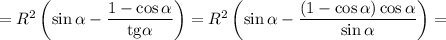

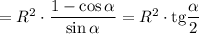
Значит, наибольшая площадь прямоугольника равна 
ответ: 

Так как в правой части стоит число 2, то значит каждое из двух слагаемых в левой части принимает значение 1.
ответ: