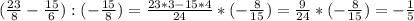
Общее расстояние от пункта А до пункта В равно 60*2= 120 км. Время, в которое он ехал со скоростью 60 км/ч неизвестно, значит обозначим его X.
Так как водитель сделал вынужденную остановку на 10 минут, то время всего пути составит 2 часа минус 10 минут, т. е. 11/6 часа. Чтобы узнать время, в которое он ехал со скоростью 80 км/ч, необходимо вычесть из 11/6 число Х. Зная скорости движения и время пути до и после остановки, можем составить уравнение.
60х+80(11/6-х) =120
Решая это уравнение, получим 4/3. Это время, которое он потратил до остановки. Умножаем 60 на 4/3, получаем расстояние 80 км. Это и будет ответом на данную задачу
Функция f(x) = x^3 - 3x имеет 2 критические точки. х = -1 - точка максимума; х = 1 - точка минимума.
Объяснение:
Решение задачи.
Критическими точками функции называются точки, в которых производная равна нулю, либо производной в этой точке не существует.
Функция f(x) = x^3 - 3x имеет производную на всем числовом интервале. Найдем точки, в которых производная функции f(x) равна нулю.
f'(x) = 3x^2 - 3;
3x^2 - 3 = 0;
3 * (x - 1) * (x + 1) = 0;
Уравнение имеет 2 корня, х = -1 и х = 1.
Функция f(x)=x^3-3x имеет 2 критические точки х = -1 и х = 1.
Определим, являются критические точки точками минимума или максимума.
f''(x) = 6x.
f''(-1) = - 6 < 0, х = -1 - точка максимума.
f''(1) = 6 > 0, x = 1 - точка минимума
2) 9/1:-15/8=9/1*-8/15=-40/5=-8