Q(1;3) принадлежит графику 3у-2х-7=0
Объяснение:
Подставим значение абсциссы и ординаты каждой точки в уравнение и решим это уравнение
М(-1;1) абсцисса х=-1; ордината у=1
3у-2х-7=0
3*1-2(-1)-7=0
3+2-7=0
5-7=0
-2≠0
Эта точка не принадлежит данному графику, потому что правая и левая часть линейного уравнения не равны между собой. -2≠0
N(0;-2) x=0; у=-2
3у-2х-7=0
3*(-2)-2*0-7=0
-6-7=0
-13≠0
Эта точка не принадлежит данному графику.
Р(0;2) х=0; у=2
3у-2х-7=0
3*2-2*0-7=0
6-7=0
-1≠0
Эта точка не принадлежит данному графику.
Q(1;3) x=1;y=3
3у-2х-7=0
3*3-2*1-7=0
9-2-7=0
0=0
Эта точка принадлежит данному графику, потому что 0=0
ответ: 0
Объяснение:
Здравствуйте!
Попробуем составить рекуррентное соотношение для чисел раскрасок.
Пусть для доски  имеем
имеем 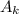 правильных раскрасок с четным числом закрашенных клеток и
правильных раскрасок с четным числом закрашенных клеток и 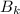 правильных раскрасок с нечетным числом закрашенный клеток, для доски
правильных раскрасок с нечетным числом закрашенный клеток, для доски
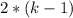 :
: 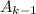 и
и 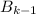 , соответственно. Определим
, соответственно. Определим 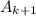 и
и 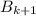 для доски
для доски 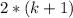 .
.
Добавим к предыдущей доске, поверх 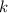 -й снизу строки,
-й снизу строки, 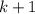 -ю строку. Вставим в нее одну из правильных раскрасок доски
-ю строку. Вставим в нее одну из правильных раскрасок доски  . У нас есть 3 варианта как мы можем закрашивать квадратики в новой строке.
. У нас есть 3 варианта как мы можем закрашивать квадратики в новой строке.
Закрашиваем левую клетку, закрашиваем правую клетку или вообще не закрашиваем. Необходимо понимать, что если мы закрашиваем левую клетку в 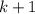 -й строке, то в
-й строке, то в 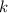 -й строке закрашен правый квадратик, либо вообще ничего не закрашено и наоборот.
-й строке закрашен правый квадратик, либо вообще ничего не закрашено и наоборот.
Пусть мы не закрасили в верхней строке ни одного квадрата, в этом случае общее число четных раскрасок : 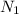 =
= 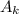 , а нечетных :
, а нечетных : 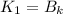
(Будем считать, что пустая раскраска входит в число четных)
Пусть мы закрасили левый квадрат в 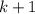 -й строке, в этом случае либо правый квадрат
-й строке, в этом случае либо правый квадрат 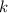 -й строки закрашен, либо вообще ничего не закрашено. То есть из всех вариантов
-й строки закрашен, либо вообще ничего не закрашено. То есть из всех вариантов 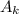 или
или 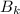 нужно вычесть те, в которых левая клетка окрашена. Из симметрии очевидно, что числа вариантов с левой и правой окрашенной клетками равны.
нужно вычесть те, в которых левая клетка окрашена. Из симметрии очевидно, что числа вариантов с левой и правой окрашенной клетками равны.
Чтобы найти число всех вариантов с окрашенной левой или правой клеткой, нужно из общего числа вариантов вычесть варианты с незакрашенными клетками.
Очевидно, что число таких вариантов равно : 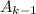 или
или 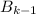
Учитывая, что с добавлением одной закрашенной клетки четность меняется, то имеем:
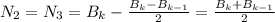 , где
, где 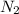 и
и 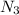 - количества правильных раскрасок с четным числом закрашенных квадратов,
- количества правильных раскрасок с четным числом закрашенных квадратов,
с закрашенным в 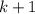 -й строке левым(индекс 2) и правым (индекс 3) квадратом.
-й строке левым(индекс 2) и правым (индекс 3) квадратом.
Аналогично:
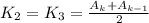 , где
, где 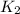 и
и 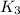 - количества правильных раскрасок с нечетным числом закрашенных квадратов, с закрашенным в
- количества правильных раскрасок с нечетным числом закрашенных квадратов, с закрашенным в 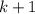 -й строке левым(индекс 2) и правым (индекс 3) квадратом.
-й строке левым(индекс 2) и правым (индекс 3) квадратом.
Таким образом :
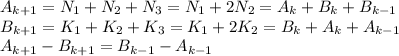
Найдем : 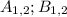
Когда 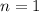 , число вариантов с нечетным числом клеток равно
, число вариантов с нечетным числом клеток равно 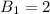 (левый и правый квадрат закрашены) . С четным же числом клеток такая комбинация только одна
(левый и правый квадрат закрашены) . С четным же числом клеток такая комбинация только одна 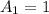 , когда ни одна клетка не закрашена (0 клеток, 0 делится на 2).
, когда ни одна клетка не закрашена (0 клеток, 0 делится на 2). 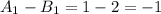
Когда 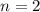 , число вариантов с нечетным числом клеток равно
, число вариантов с нечетным числом клеток равно 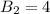
(все варианты закрасить одну клетку, поскольку 3 клетки всегда будут вплотную) . С четным числом клеток имеем 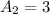 таких комбинаций ( две комбинации с двумя клетками по диагонали и одна комбинация с незакрашенными клетками).
таких комбинаций ( две комбинации с двумя клетками по диагонали и одна комбинация с незакрашенными клетками). 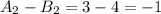
Из полученного выше свойства имеем:
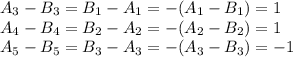
И так далее, то есть 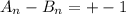
Таким образом, сумма возможных значений 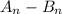 равна:
равна:
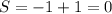
Если вам понравилось решение, ставь лайк и отметь его лучшим.