Сколько существует четырехзначных чисел, в записи которых ровно три цифры? объясните,,как решать такие .

👇

Ответ:

Ytbjfdg

15.06.2021

ответ 36+1 = 37 . т.к. 1000 (0 тоже цифра) вот начинается с 111х 11х1 1х11 х111 .. .и так до х999 х - любая цифра ... 4*9=36 на 9 т.к. 123456789 -цифры

4,6(82 оценок)

Ответ:

nastyaswan1405

15.06.2021

3 совпадающие цифры это значит 111 или 222 ... 999

с 111 может быть 1110, (1111- не подходит т.к там 4 совпад цифр), 11121119, -9 вариантов

1101, 11211191-еще 9 вариантов

1011, 12111911- еще 9 вариантов

0111,2111,31119111 еще 9 вариантов, следовательно существую 36 вариантов для трех одинаковых цифр 1

также для цифр от 2-до 9, следовательно 36*9= 324 варианта

и еще один вариант с тремя нолями 1000, следовательно существует 325 вариантов четырехзначных чисел

4,5(80 оценок)

Открыть все ответы

Ответ:

LentaKuim

15.06.2021

Дано: sinx-siny=m; cosx+cosy=n. Найти: sin(x-y) и cos(x-y).
Решение:
1. Воспользуемся формулами разность синусов и сумма косинусов:
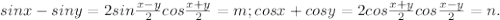
$sinx-siny=2sin \frac{x-y}{2}cos \frac{x+y}{2}=m; cosx+cosy=2cos \frac{x+y}{2}cos \frac{x-y}{2}=n.$
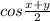Заметим, что оба равенства содержат один и тот же член: $cos \frac{x+y}{2}$ . Выразим его из обоих равенств:
$cos \frac{x+y}{2}= \frac{m}{2sin \frac{x-y}{2}};cos \frac{x+y}{2}= \frac{n}{2cos \frac{x-y}{2}}.$
В получившихся равенствах левые части равны, значит, равны и правые части:
$\frac{m}{2sin \frac{x-y}{2}}= \frac{n}{2cos \frac{x-y}{2}}$ .
Преобразуем данное равенство:
$\frac{2sin \frac{x-y}{2}}{2cos \frac{x-y}{2}}= \frac{m}{n};$
$\frac{sin \frac{x-y}{2}}{cos \frac{x-y}{2}}= \frac{m}{n};$
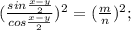
$( \frac{sin \frac{x-y}{2}}{cos \frac{x-y}{2}})^{2}=( \frac{m}{n})^{2};$
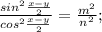
$\frac{sin^{2} \frac{x-y}{2}}{cos^{2} \frac{x-y}{2}}= \frac{m^{2}}{n^{2}};$
Теперь используем формулы понижения степени синуса и косинуса:
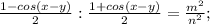
$\frac{1-cos(x-y)}{2}: \frac{1+cos(x-y)}{2}= \frac{m^{2}}{n^{2}};$
Преобразуем данное равенство:
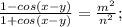
$\frac{1-cos(x-y)}{1+cos(x-y)}= \frac{m^{2}}{n^{2}};$
n²(1-cos(x-y))=m²(1+cos(x-y));
n²-n²cos(x-y)=m²+m²cos(x-y);
m²cos(x-y)+n²cos(x-y)=n²-m²;
cos(x-y)(m²+n²)=n²-m²;
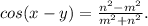
$cos(x-y)= \frac{n^{2}-m^{2}}{m^{2}+n^{2}}.$
Используя основное тригонометрическое тождество, выразим sin(x-y):
$sin(x-y)= \sqrt{1-( \frac{n^{2}-m^{2}}{m^{2}+n^{2}})^{2}}.$
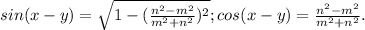
ответ: $sin(x-y)= \sqrt{1-( \frac{n^{2}-m^{2}}{m^{2}+n^{2}})^{2}};cos(x-y)= \frac{n^{2}-m^{2}}{m^{2}+n^{2}}.$

4,5(35 оценок)

Ответ:

taniaovchinnik

15.06.2021

1. Примем зарплату работника за x. Имеем:
x * ((100 + 10) / 100) * ((100 + 20) / 100) = (110 * 120) / 10000 =
13200 / 10000 = 132 / 100 = (100 + 32) / 100, то есть зарплата повысилась на 32%.
2. Постройте пятиконечную звезду и расставьте яблони на каждом пересечении её граней.
3. В январе 31 день, то есть 4 недели и три дня. Если в январе четыре пятницы и четыре понедельника, то оставшиеся 3 дня не могут быть ни пятницей, ни понедельником. Такое возможно, если месяц начался со вторника.
4. Из условия задачи имеем: Пётр не из 4 - го, не из 5 - го и не из 7 - го класса, значит он из 6 - го. Николай не из 6 - го, не из 7 - го и не из 5 - го класса, значит он из 4 - го. Вася не из 5 - го, не из 6 - го и не из 4 - го, значит он из 7 - го. Степан не из 4 - го, не из 6 - го и не из 7 - го, значит он из 4 - го.
5. Весь отрезок 50 сантиметров. Вычтем из этого 30 и найдём, что сумма половин крайних отрезков равна 20. Вычтем данное число из 30:
30 - 20 = 10 и разделим пополам: 10 / 2 = 5 - искомое расстояние.

4,8(59 оценок)

Это интересно:

Кулинария-и-гостеприимство

23.04.2021

Освежающий и полезный напиток: лимонад из лаймов и имбиря...

Здоровье

23.09.2021

Как сохранить здоровые и крепкие зубы...

Финансы-и-бизнес

09.05.2023

Как эффективно организовать сбор средств для благотворительных целей?...

Компьютеры-и-электроника