


task/29635004 Найди наибольший отрицательный корень уравнения sin²x - 5sinx*cosx + 2 = 0
sin²x - 5sinx*cosx + 2 = 0 ⇔sin²x - 5sinx*cosx + 2(sin²x+cos²x) = 0 ⇔
3sin²x - 5sinx*cosx +2cos²x = 0 || : cos²x ≠ 0 || ⇔3tg²x -5tgx +2 =0 ⇔
[ tgx = 1 ; tgx =2/3 . ⇔ [ x = π/4 +πn ; x =arctg(2/3) + πn , n∈ℤ .
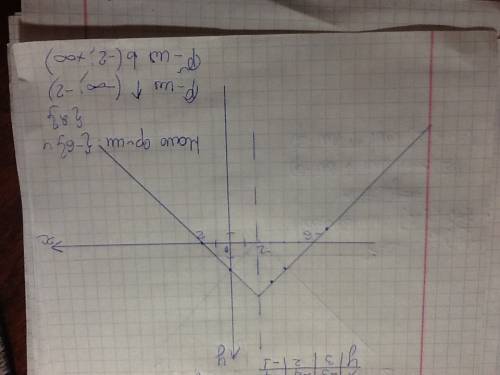
Корни отрицательные при n ≤ -1. Между максимальными отрицательными корнями имеет место неравенство: arctg(2/3) - π < π/4 - π < 0 . * * * arctg(2/3) < arctg1 = π/4 * * *
ответ : - 3π/4.
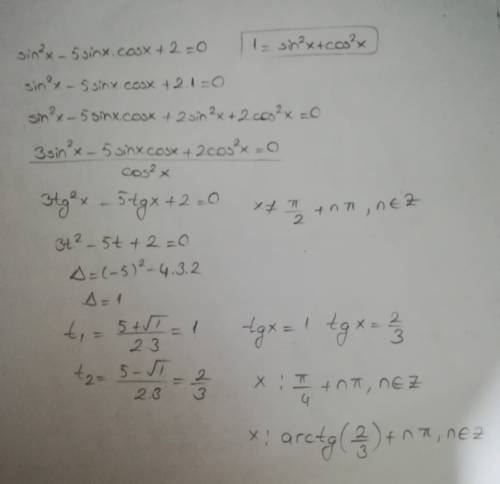
cos (3 * x) - cos (5 * x) = sin (4 * x);
Разложим левую часть уравнения на множители, применив формулу суммы углов.
-2 * sin ((3 * x - 5 * x)/2) * sin ((3 * x + 5 * x)/2) = sin (4 * x);
-2 * sin (-2 * x/2) * sin (8 * x/2) = sin (4 * x);
-2 * sin (-x) * sin (4 * x) = sin (4 * x);
2 * sin x * sin (4 * x) = sin (4 * x);
Перенесем все значения на одну сторону.
2 * sin x * sin (4 * x) - sin (4 * x) = 0;
sin (4 * x) * (2 * sin x - 1) = 0;
1) sin (4 * x) = 0;
4 * x = pi * n;
x = pi/4 * n;
2) 2 * sin x - 1 = 0;
2 * sin x = 1;
sin x = 1/2;
x = (-1)^n * pi/6 + pi * n.
Объяснение: