ух сколько ненужных лишних накруток
снимает нечетные степени , совершенно очевидно, что если число больше другого, то и в 9-й степени они будут также соотносится
∛x + 3^(x+1) - 3 > ∛x + 9^x - 3^x
∛x взаимно уничтожатся , никаких ограничений на корни нечетной степени неи надо (на четной надо)
9^x = (3^x)^2
3^x=t
3t - 3 > t^2 - t
t^2 - 4t + 3 < 0
D = 16-12 = 4
t12=(4+-2)/2 = 1 3
(t-1)(t-3) < 0
метод интервалов
(1) (3)
t∈(1 3)
t>1 3^x>1 3^x>3^0 x>0
t<3 3^x < 3 x < 1
x∈(0, 1)
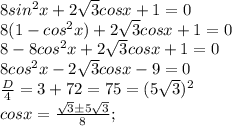
Так как функция косинус по модулю не превосходит единицы в поле действительных чисел, то выбираем 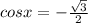
Далее решаем это уравнение:
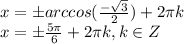
По условию нужно найти корни на промежутке ![[-\frac{7\pi}{2}; -2\pi]](/tpl/images/1359/8515/36df4.png) .
.
Это можно сделать несколькими например, с неравенства:
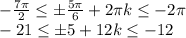
Рассмотрим случай, когда 5 имеет знак "плюс":
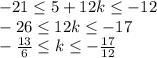
Очевидно, что из целых k подходит k = -2.
Теперь рассмотрим случай, когда 5 имеет знак "минус":
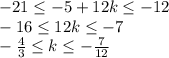
k = -1 нам подходит.
Теперь подставляем полученные k в серию корней:
1) Когда плюс - k = -2, т. е. 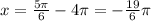
2) Когда минус - k = -1, т. е. 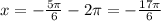
ответ: а) 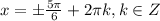
б) 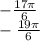
Найдем корни:
Так как сумма крайних коэффициентов равна среднему коэффициенту, то один из корней равен -1, а второй 8/(-1)=-8. Получим:
t^2+9t+8=(t+1)(t+8)=(x^4+1)(x^4+8)