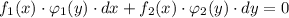
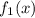и 
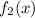зависят только от переменной "х" , а функци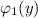и 
и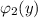 
зависят только от переменной "у" . Указывается на то, что диффер. уравнение допускает обособление (разделение) переменных только тогда, когда перед дифференциалами (dx и dy) стоят функции, являющиеся произведениями двух других функций, одна из которых зависит только от "х" , а вторая зависит только от "у" . 
. 
.
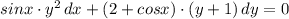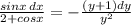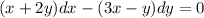, то переменные уже нельзя разделить, так как нельзя функции, стоящие перед dx и dy,представить в виде произведения 
.
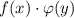ax²+bx+c=a(x-x₁)(x-x₂)
Решаем квадратное уравнение, где
a=3
b=-11y
c=-4y²
D=11²y²-4*3(-4y²)=121y²+48y²=169y²
√D=13y
x₁=(11y-13y)/(2*3)=-y/3
x₂=(11y+13y)/(2*3)=4y
Значит, разложение имеет вид
3x²-11xy-4y²=3(x+y/3)(x-4y)
ответ: 3(x+y/3)(x-4y)
Может, тройку внести в скобку? Красивее тогда будет
3(x+y/3)(x-4y)=(3+y)(x-4y)
ответ: (3+y)(x-4y)
Да, так, я думаю, правильнее.