Объяснение:
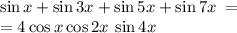
Проведем доказательство тождества следующим образом:
- проведем равносильные преобразования левой части доказываемого тождества;
- если в итоге преобразований левая часть примет ту же форму что и правая часть - тождество доказано.
Итак - левая часть:
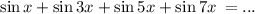
Сгруппируем следующим образом:
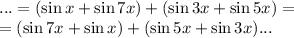
Воспользуемся формулой суммы синусов:
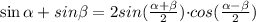
Поочередно сложим группы внутри скобок:
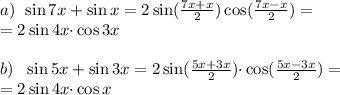
Тогда вся левая часть примет вид:
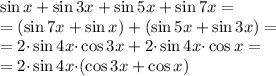
для преобразования суммы косинусов в скобках воспользуемся такой формулой:
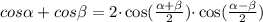
Выражение примет вид:
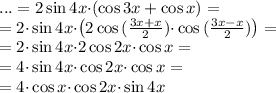
В результате преобразований левая часть приняла тот же вид что и правая.
Тождество доказано.
для меня это самое понятное... надеюсь
Объяснение:
Предположим, что нам нужно составить квадратное уравнение, корнями которого были бы числа x1 и x2. Очевидно, что в качестве искомого уравнения можно выбрать уравнение
a(х — x1)(х — x2) = 0, (1)
где а — любое отличное от нуля действительное число. С другой стороны, каждое квадратное уравнение с корнями x1 и x2 можно записать в виде (1).
Таким образом, формула (1) полностью решает поставленную выше задачу. Из всех квадратных уравнений корни x1 и x2 имеют уравнения вида (1) и только, они.
Пример. Составить квадратное уравнение, корни которого равны 1 и — 2.
ответ. Корни 1 и —2 имеют все квадратные уравнения вида
а(х — 1)(х + 2) = 0,
или
ах2 + ах — 2а = 0,
где а — любое отличное от нуля действительное число. Например, при а = 1 получается уравнение
х2 + х — 2 = 0.
12(х + 4) + 15х = 534
12х + 48 + 15х = 534
27х = 486
х = 18
в первом зале 12*(18+4) = 264
во втором 15*18=270
2. пусть х литров вылили из первой цистерны
3.5(200-х) = 640-2х
700-3.5х=640-2х
1.5х=60
х=40
из первой 40 литров
из второй 40*2=80