В решении.
Объяснение:
И пунктов А и В, расстояние между которыми 225 км, выехали одновременно навстречу друг другу два велосипедиста. Один велосипедист ехал со скоростью 20 км/ч, а другой — со скоростью 25 км/ч. Через t ч расстояние между ними было S км.
1. Задайте формулой зависимость S от t.
Рассмотри два случая:
а) велосипедисты еще не встретились ;
b) встреча произошла, но велосипедисты продолжают движение.
а) S₁ = 20t;
S₂ = 25t.
S = 225 - (20+25)t.
b) S = 45t - 225
2. Через какое время после начала движения расстояние между велосипедистами станет равно 45 км?
а)
S = 225 - (20+25)t.
225 - (20+25)*t = 45
225 - 45t = 45
-45t = 45 - 225
-45t = -180
t = -180/-45
t = 4 (часа).
б)
S = 45t - 225
45 = 45t - 225
-45t = -225 - 45
-45t = -270
t = -270/-45
t = 6 (часов).
а) t₁= 4 часа;
б) t₂= 6 часов.
Введите задачу...
Алгебра Примеры
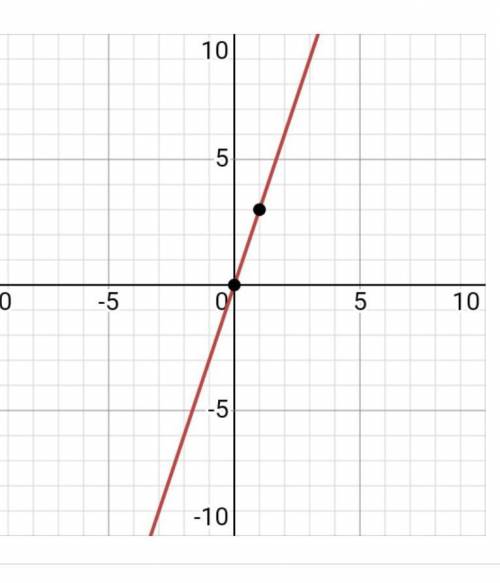
Популярные задачи Алгебра График y=3x
y
=
3
x
Воспользуемся уравнением для пучка прямых, проходящих через заданную точку для того, чтобы найти угловой коэффициент и точку пересечения с осью Y.
Нажмите, чтобы увидеть больше шагов...
Угловой коэффициент:
3
пересечение с осью Y:
0
Любую прямую можно построить при двух точек. Выберем два значения
x
и подставим их в уравнение, чтобы определить соответствующие значения
y
.
Нажмите, чтобы увидеть больше шагов...
x
y
0
0
1
3
Построим прямую с углового коэффициента и пересечения с осью Y или опираясь на две точки прямой.
Угловой коэффициент:
3
пересечение с осью Y:
0
x
y
0
0
1
3
Замена переменной
х²-х=t
получаем уравнение
t²+t=6
t²+t-6=0
D=1+24=25
t=(-1-5)/2 = -3 или t=(-1+5)/2 = 2
Возвращаемся к переменной х:
х²-х=-3 или х²-х=2
решаем ещё два квадратных уравнения
х²-х+3 = 0 D=1-12<0 уравнение не имеет корней
и
х²-х-2=0 D=1+8=9 х = -1 или х = 2
ответ. -1;2
б) (3х² + 2х)² – 4(3х² + 2х) – 5 = 0;
Замена (3х²+2х)=t
t²-4t-5=0
D=16+20=36
t=(4-6)/2 = -1 или t=(4+6)/2 = 5
Возвращаемся к переменной х:
3х² + 2х = -1 или 3х² + 2х = 5
решаем ещё два квадратных уравнения
3х² + 2х +1= 0 D=4-12<0 уравнение не имеет корней
и
3х² + 2х -5 = 0 D=4+60=64 х = (-2-8)/6=-5/3 или х =(- 2+8)/6=1
ответ. -5/3; 1
в) (х² + х + 1)(х² + х + 2) = 12;
Замена переменной
х²+х+1 = t
х²+х+2 = t + 1
получаем уравнение
t(t+1)=12
t²+t-12=0
D=1+48=495
t=(-1-7)/2 = -4 или t=(-1+7)/2 = 3
Возвращаемся к переменной х:
х²+х+1 =-4 или х² +х + 1 = 3
решаем ещё два квадратных уравнения
х²+ х + 5 = 0 D=1-20<0 уравнение не имеет корней
и
х² + х - 2 =0 D=1+8=9 х = 1 или х = - 2
ответ. 1; -2
г) (х²– 4х + 1)(х² – 4х – 3) = 12.
Замена переменной
х² - 4х - 3 = t
х²– 4х + 1= t + 4
получаем уравнение
t(t+4)=12
t²+4t-12=0
D=16+48=64
t=(-4-8)/2 = -6 или t=(-4+8)/2 = 2
Возвращаемся к переменной х:
х²-4х - 3 = -6 или х²- 4х - 3 = 2
решаем ещё два квадратных уравнения
х²- 4х+3 = 0 D=16-12=4
x = (4-2)/2=1 или x = (4+2)/2=3
и
х²-4х-5 = 0 D=16 +20 = 36 х = (4-6)/2= -1 или х=(4+6)/2 =5
ответ. -1; 1 ; 3; 5