Используя формулу двойного угла, имеем:
2 sin x cos x + sin x = 0
sin x(2cos x + 1) = 0
sin x = 0 2 cos x +1 = 0
x₁=πn, n∈Z cos x = -1/2
x₂=±2π/3 + 2πn, n∈Z
В заданном промежутке находится х=2π/3, т.е. х=120°
ответ. 120°
а) 1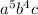7 
г) -7
Объяснение:
Одночлен — произведение, состоящее из числового множителя и одной или нескольких переменных, взятых каждая в неотрицательной степени.
Неотрицательные числа - это все положительные числа и 0.
а) 17 - числовой множитель, умноженный на 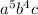- несколько переменных, каждая из которых в неотрицательной степени: ПОДХОДИТ
б) здесь сумма одночленов: НЕ ПОДХОДИТ
в) -23 - числовой множитель, умноженный на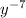 
- переменная, взятая в отрицательной степени: НЕ ПОДХОДИТ
г) -7 - числовой множитель, умноженный на переменную в степени 0: ПОДХОДИТ
Исследовать функцию f (x) = 11x/(16+x²) и построить ее график.
1. Область определения функции - вся числовая ось, так как знаменатель не может быть равен нулю.
2. Функция f (x) = 11x/(16+x²) непрерывна на всей области определения. Точек разрыва нет.
3. Четность, нечетность, периодичность:
f(–x) = 11*(–x)/(16+(–x)²) = –11x(16+x²) ≠ f(x)
f(–x) = 11*(–x)/(16+(–x)²) = –(11x(16+x²)) = –f(x)
Функция является четной. Функция непериодическая.
4. Точки пересечения с осями координат:
Ox: y=0, 11x/(16+x²) = 0 ⇒ x=0. Значит (0;0) - точка пересечения с осью Ox.
Oy: x = 0 ⇒ y = 0. Значит (0;0) - точка пересечения с осью Oy.
5. Промежутки монотонности и точки экстремума:
Находим производную заданной функции.x = 4, x = -4 критические точки.
Интервалы возрастания и убывания функции:6. Найдем точки перегибов, для этого надо решить уравнение
\frac{d^{2}}{d x^{2}} f{\left (x \right )} = 0
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
\frac{d^{2}}{d x^{2}} f{\left (x \right )} =
Вторая производная
\frac{22 x}{\left(x^{2} + 16\right)^{2}} \left(\frac{4 x^{2}}{x^{2} + 16} - 3\right) = 0
Решаем это уравнение
Корни этого уравнения
x_{1} = 0
x_{2} = - 4 \sqrt{3}
x_{3} = 4 \sqrt{3}
7. Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках
Выпуклая на промежутках
8. Искомый график функции дан в приложении.
2sinxcosx + sinx = 0
sinx(2cosx+1) = 0
Разбиваем на два уравнения:
sinx = 0 cosx = - 1/2
x = Пk x = +- 2П/3 + 2Пn
В указанный в условии промежуток попадает только один угол:
х = 2П/3 = 120 град.
ответ: 120 град.