Пусть первый токарь в час изготавливал х деталей, тогда второй - (х-3) детали. Первый токарь изготовит 40 деталей за 40/х часов, а второй - за 40/(х-3) часов. Зная, что второй будет работать на 3 часа больше, составляем уравнение:
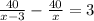 x≠0, x≠3
x≠0, x≠3
40х-40х+120=3х(х-3)
3х²-9х-120=0
х²-3х-40=0
х₁=-5 - не подходит
х₂=8
ответ. 8 деталей.
2,5 (часа) пароход по течению реки.
1,5 (часа) пароход против течения реки.
Объяснение:
Пароход по течению реки и против течения путь 68 км за 4 часа. Сколько времени он двигался против течения и по течению реки (отдельно), если по течению он двигался со скоростью 20 км / ч, а против течения - 12 км / ч?
Формула движения: S=v*t
S - расстояние v - скорость t – время
х - расстояние по течению
у - расстояние против течения
х/20 - время по течению
у/12 - время против течения
По условию задачи составляем систему уравнений:
х+у=68
х/20 + у/12 =4
Преобразуем второе уравнение, умножим его на 240, чтобы избавиться от дроби:
12х+20у=960/4 для упрощения:
3х+5у=240
Выразим х через у в первом уравнении, подставим выражение во второе уравнение и вычислим у:
х=68-у
3(68-у)+5у=240
204-3у+5у=240
2у=240-204
2у=36
у=18 (км) - расстояние против течения.
х=68-у
х=68-18
х=50 (км) - расстояние по течению.
Скорость по течению и против течения известны, можем вычислить время:
50/20=2,5 (часа) пароход по течению реки.
18/12=1,5 (часа) пароход против течения реки.
знаки тригонометрических функций по четвертям:
tg ; ctg II I
- +
+ -
III IV
tg 189* двигаемся против часой стрелке на 189*, попадаем в III четверть, смотрим знак, видим +, но нам по заданию нужен противоположный, -tg189* <0 (минус)
tg 269* двигаемся от 0 против часовой стрелке на 269*, попадаем в III четверть, смотрим знак, видим +, tg269* >0
-tg 269* <0
отрицательное число ещё уменьшаем, получаем:
-tg189° - tg269° < 0 (знак минус)
Пусть х - искомая производительность 1-го токаря. Тогда (х-3) - производительность 2-го.
Уравнение для времени:
40/(х-3) - 40/х = 3
40х - 40х + 120 = 3х^2 - 9x
x^2 - 3x - 40 = 0
x1 = -5 - не подходит.
х2 = 8.
ответ: 8 дет/час.