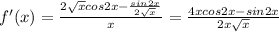Question

Спроизводной : 1. найдите координаты точек пересечения с осями координат касательных к графику функции , имеющий угловой коэффициент 25 2. найти производную функцию:

Answer 1

1) Y' = (3x-9-3x+5)/(x-3)^2  =  (-4)/(x-3)^2

Видим, что производная на всей области определения отрицательна. Значит не существует касательной к графику этой ф-ии, имеющей положительный угловой коэффициент! Либо коэффициент не 25, а (-25), либо неверное условие самой ф=ии.

ответ: нет  решений. 

2) $f'(x)=\frac{2\sqrt{x}cos2x-\frac{sin2x}{2\sqrt{x}}}{x}=\frac{4xcos2x-sin2x}{2x\sqrt{x}}$

Answer 2

1. Находим производную функции.

у'=((3x-5)' (x-3) - (3x-5)(x-3)') / (x-3)² = (3x-9-3x+5)/(x-3)² = -4/(x-3)²

Значение производной число отрицательное ⇒ нет такой касательной, имеющей положительный коэффициент.

ответ. решений нет. 

2. $f'(x) = \frac{(sin2x)'\sqrt{x} - sin 2x(\sqrt{x})'}{(\sqrt{x})^2} = \frac{2cos 2x \cdot\sqrt{x} - \frac{sin 2x}{2\sqrt{x}}}{x} = \frac{4xcos 2x-sin 2x}{2x\sqrt{x}}$