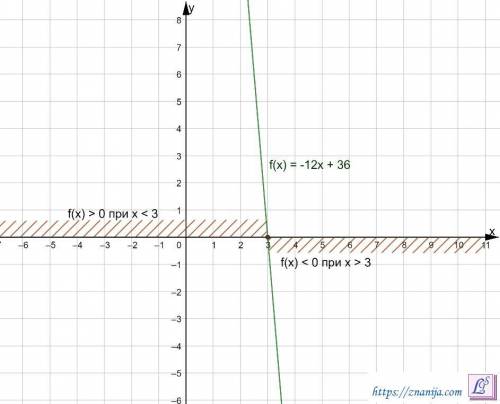
Функция f(x) = -12x + 36 убывающая.
f(x) = 0 при x = 3.
f(x) > 0 при x ∈ (-∞; 3)
f(x) < 0 при x ∈(3; +∞)
Объяснение:
f(x) = -12x + 36
Это линейная функция, ее график прямая линия. Общий вид линейной функции f(x) = kx + b.
Коэффициент k определяет угол наклона прямой к оси ОХ.
k = -12, k < 0, прямая проходит через II - IV четверти. (k < 0, угол между прямой и положительный направлением оси ОХ тупой)
⇒ Функция f(x) = -12x + 36 убывающая.
f(x) = 0; -12x + 36 = 0; 12x = 36; x = 3
f(x) = 0 при x = 3.
f(x) > 0 при x ∈ (-∞; 3)
f(x) < 0 при x ∈(3; +∞)
Объяснение:
Функция f(x) = -12x + 36 убывающая.
f(x) = 0 при x = 3.
f(x) > 0 при x ∈ (-∞; 3)
f(x) < 0 при x ∈(3; +∞)
Объяснение:
f(x) = -12x + 36
Это линейная функция, ее график прямая линия. Общий вид линейной функции f(x) = kx + b.
Коэффициент k определяет угол наклона прямой к оси ОХ.
k = -12, k < 0, прямая проходит через II - IV четверти. (k < 0, угол между прямой и положительный направлением оси ОХ тупой)
⇒ Функция f(x) = -12x + 36 убывающая.
f(x) = 0; -12x + 36 = 0; 12x = 36; x = 3
f(x) = 0 при x = 3.
f(x) > 0 при x ∈ (-∞; 3)
f(x) < 0 при x ∈(3; +∞)
Стандартный вид числа это такая его запись, где модуль числа ≥ 1 и <10 умножен на 10 в целой степени, которая может быть положительной, отрицательной или нулем.
Стандартный вид числа — это выражения вида a,bc... · 10ᵏ, где a, b, c, ... — обычные цифры, причем a ≠ 0. Число k — целое.
Запишем числа в стандартном виде.
0,0055= 5,5·10<10⁻³
4200,3=4,2003·10³
347,37=3,4737·10²
0,03041=3,041·10⁻²
Число 10 ставим в ту степень, на сколько разрядов переносим запятую.
Если приводим к стандартному виду число меньше нуля, знак степени при 10 тоже меньше нуля, т.е. отрицательный. Если приводим к стандартному виду число больше нуля, знак степени при 10 тоже больше нуля, т.е. положительный.
Цитата:" Важно!
Из определения стандартного вида числа следует, что в стандартном виде в целой части числа (до запятой) может содержаться только одна цифра. Все остальные цифры должны стоять после (справа от) запятой."