1) Из условия составим систему уравнений для нахождения b1 и q:
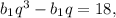
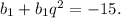
Поделив уравнения, получим:
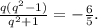
Домножив на общий знаменатель и приведя подобные члены, получим кубическое уравнение для нахождения q:
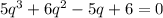
Подбором сразу находим один корень: q = -2.
Поделив кубический многочлен на (q+2), получим:

Корень (-2) - единственный, так как второй множитель корней не имеет (D<0).
Итак q= -2. Из второго уравнения системы найдем b1:
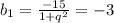
Теперь находим искомую сумму:

ответ: 255
2. Исходя из условия, составим систему:
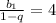
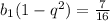
Или разделив второе на первое, получим:
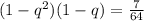
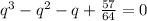
По условию q- рациональная дробь. Подбором находим рациональный корень: q = 3/4.
Тогда из первого уравнения системы находим: b1 = 1
Тогда:
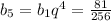
ответ: 81/256
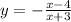
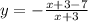
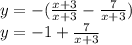
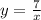 , сдвинутая на 3 влево по оси x и на 1 вниз по оси y.
, сдвинутая на 3 влево по оси x и на 1 вниз по оси y.
1) a1q^3 - a1q=18
a1+a1q^2=15
из второго уравнения, имеем
a1(1+q^2)=15 => a1=15/(1+q^2)
подставим в первое уравнение значение a1,получим
15 q^3/(1+q^2)-15q/(1+q^2)=18
15q^3-15q=18(1+q^2)
15q^3-18q^2-15q-18=0
5q^3-6q^2-5q-6=0
5q^3-10q^2+4q^2-8q+3q-6=0
(5q^3-10q^2)+(4q^2-8q)+(3q-6)=0
5q^3(q-2)+4q(q-2)+3(q-2)=0
(q-2)(5q^2+4q+3)=0
a) q-2=0 => q=2
б) 5q^2+4q+3=0
D=b^2-4ac=-44 - нет решений
итак, a1=15/(1+q^2)=15/(1+4)=3
то есть, a1=3 и q=2
s8=a1*(1-q^8)/(1-q)=3*(1-2^8)/(1-2)=3*255=765