Question

При каких значениях а уравнение (а-1)хкв+(2а-3)х-3а+4=0 имеет два напишите решение! )

Answer 1

$(a-1)x^2+(2a-3)x-(3a-4)=0$

Чтобы квадратное уравнение имело два корня, необходимо, чтобы дискриминант был положительным, и коэффициент при x^2 был не равен 0. То есть сразу имеем: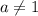 $a\neq1$

$D\ =\ (2a-3)^2+4(a-1)(3a-4)\ =\ 4a^2-12a+9+12a^2-28a+160$

$16a^2-40a+250,\ \ \ \ (4a-5)^20,\ \ \ \ a\ \neq\ 1,25$

При а = 1,25 уравнение будет иметь один корень, что противоречит условию.

Кстати при а=1 (см. выше) уравнение вырождается в линейное и тоже имеет только один корень. То есть надо исключить два значения а: 1 и 1,25.Области будут выглядеть так:

а принадлежит (-бескон; 1)v(1; 1,25)v(1,25; бескон).

Answer 2

Δ>0 и a≠0 чтобы были два корней 

Δ=b²-4ac

a=a-1

b=2a-3

c=-3a+4

a-1≠0

a≠1 

Δ=(2a-3)²-4(a-1)*(-3a+4)

Δ=4a²-12a+9-4(-3a²+4a+3a-4)

Δ=4a²-12a+9+12a²-16a-12a+16

Δ=16a²-40a+25 

16a²-40a+25>0

16a²-20a-20a+25>0

4a(4a-5)-5(4a-5)>0

(4a-5)(4a-5)>0

(4a-5)²>0 

поэтому: 

4a-5≠0

4a≠5

a≠5/4 

a∈R\{1,5/4}