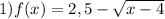
Выражение, стоящее под корнем чётной степени, должно быть неотрицательным, то есть ≥ 0 .
x - 4 ≥ 0
x ≥ 4
ответ : x ∈ [4 ; + ∞)
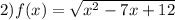
x² - 7x + 12 ≥ 0
(x - 3)(x - 4) ≥ 0
+ - +
____________[3]___________[4]_________
//////////////////////// ////////////////////
ответ : x ∈ (- ∞ ; 3] ∪ [4 ; + ∞)
3) Знаменатель дроби не должен равняться нулю, так как на ноль делить нельзя.
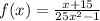
25x² - 1 ≠ 0
25x² ≠ 1
x² ≠ 1/25
x₁ ≠ - 1/5 x₂ ≠ 1/5
ответ : x ∈ (- ∞ ; - 1/5) ∪ (- 1/5 ; 1/5) ∪ (1/5 ; + ∞)
1)3b^2-10b-10/20b^4
2) 5x-5/x^2-25.
3) 2/x^2-3x
4) 1+6a/a+2
Объяснение:
1)Надо записать под общим знаменателем 20b^4. И подставлять в числитель. 5b*(3b-2)-2(6b^2-5)/20b^4. 15b^2-10b-12b^2+10/20b^4.
2) общий знаменатель x^2-25.
X-5+4x/x^2-25. 5x-5/x^2-25
3) рассписываем x^2-9 как (X-3)(X+3). И из x^2-3x выносим X. X(X-3). и общим знаменателем будет X(X-3)(X+3). Тогда:
4X-2X+6/X(X-3)(X+3). 2X+6/X(X-3)(X+3). 2(X+3)/X(X-3)(X+3). Сокращаем (X+3).
2/X^2-3X.
4) общий знаменатель a+2.
1-3a^2+3a^2+6a/a+2. -3a^2 и +3a^2 сокращаются. 1+6a/a+2
Одз :- sin 2x≥0;⇒ sin 2x ≤0; pi + 2pik ≤ 2x ≤ 2pi k;
pi/2+ pik ≤ x ≤ pik
То есть подходят корни только 2 -й и 4-й коорд. четвертей.
0,25 - cos 2x = (-sin 2x)^2;
0,25 - cos 2x = sin^2(2x);
0,25 - cos 2x = 1 - cos^2(2x);
cos^2(2x) - cos 2x - 0,75=0;
D= 1+3= 4 = 2^2;
cos 2x = - 1/2; ⇒2 x = +-2pi/3 + 2pik;⇒ x = +-pi/3 + pik.
cos 2x = 3/2 >1; ⇒ x- пустое множество.
Сравним с одз
Видно, что х = pi/3 + pik не подходит по одз.
ответ : х = - pi/3 + pik; k-Z