Question

1)найдите наибольший член последовательности a_n=(n^2-14)/2^n 2)найдите седьмой и четырнадцатый члены возрастающей прогрессии, если их сумма равна 21, а произведение десятого и одиннадцатого членов этой прогрессии равно 98

Answer 1

1). $a_{n}\ =\ \frac{n^2-14}{2^n},\ \ \ \ a'(n)=\frac{2n*2^n\ -\ (n^2-14)*2^n*ln2}{2^{2n}}\ =$

$=\ \frac{2n-(n^2-14)ln2}{2^n}\ =\ 0,\ \ \ \ln2*n^2-2n-14ln2\ =\ 0,$

$D=4+56ln^22,\ \ \ \ n=\frac{2+\sqrt{4+56ln^22}}{2ln2}\ \approx\ 5,45$

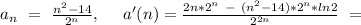
Значит нам надо проверить n = 5, и n = 6, и выбрать наибольшее:

Проверка показывает, что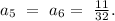 $a_{5}\ =\ a_{6}= \ \frac{11}{32}.\$

ответ: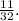 $\frac{11}{32}.$

2) Пусть х - 7-ой член последовательности, тогда х*q^7  - 14-й член последовательности, а xq^3 и xq^4  - 10-ый и 11-ый члены последовательности.   Из условия получим систему:

$x(1+q^7)\ =\ 21$      $x\ +\ \frac{98}{x}\ =\ 21$

$x^2\ q^7\ =\ 98$      $q^7\ =\ \frac{98}{x^2}$

$x^2\ -\ 21x\ +\ 98\ =\ 0,\ \ \ \ x_{1}=7,\ \ \ x_{2}=14$

Тогда:  $q_{1}^7\ =\ 2,\ \ \ q_{2}^7\ =\ 0,5$

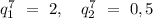
Второе значение не подходит по условию возрастания последовательности.

Итак имеем: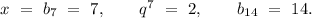  $x\ =\ b_{7}\ =\ 7,\ \ \ \ \ \ q^7\ =\ 2,\ \ \ \ \ \ b_{14}\ =\ 14.$

ответ: 7;  14.