Объяснение:
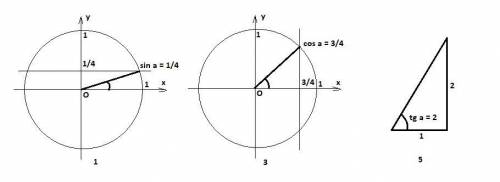
1) sin a = 1/4
Строим окружность единичного радиуса.
По оси Oy откладываем отрезок длиной 1/4 и проводим горизонтальную линию.
Она пересекается с окружностью в 1 четверти.
Рисуем линию из центра координат.
Получаем угол sin a = 1/4.
3) cos a = 3/4
Строим окружность единичного радиуса.
По оси Ox откладываем отрезок длиной 3/4 и проводим вертикальную линию.
Она пересекается с окружностью в 1 четверти.
Рисуем линию из центра координат.
Получаем угол cos a = 3/4.
5) tg a = 2
Это совсем просто.
Строим прямоугольный треугольник, у которого один катет
a = 2, а второй катет b = 1.
Угол против катета а и будет иметь tg a = 2/1 = 2
Примерные рисунки прилагаются.
Построить точно я, к сожалению, не могу - у меня нет программы построения фигур с точными размерами.
x^2-6x+19=0
a=1 b=-6 c=19
D=b^2-4ac=(-6)^2-4*1*19=36-76<0, следовательно, решений нет. ответ: решений нет.
x^2-6x+9=0
a=1 b=-6 c=9
D=b^2-4ac=(-6)^2-4*1*9=36-36=0, следовательно, ур-е имеет единственный корень, который мы можем вычислить по формуле: x=(-b)/2a=-(-6)/2*1=6/2=3 ответ: 3.
x^2-6x=0
Вынесем "х" за скобку:
x(x-6)=0
Произведение равно 0 тогда, когда хотя бы один из множителей равен 0. Следовательно:
x=0 или x-6=0 x=6 ответ: 0, 6.
x^2-6=0
x^2=6
Извлекаем квадратный корень из двух частей и получаем:
![x=\sqrt[2]{6} \\x=-\sqrt[2]{6}](/tpl/images/4424/0353/fa5da.png)
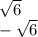
пусть 7⁷⁷>77⁷, тогда 7⁷⁷-77⁷>0
7⁷⁷-(7*11)⁷>0
7⁷⁷-7⁷ *11⁷>0
7⁷ *(7⁷⁰-11⁷)>0
7⁷ *((7¹⁰)⁷-11⁷)>0
7⁷>0. (7¹⁰)⁷-11⁷>0
=> 7⁷⁷>77⁷