27.
Объяснение:
Пусть х - цифра из разряда десятков неизвестного двузначного числа,
у - цифра из разряда единиц этого числа,
тогда неизвестное двузначное число можно записать в виде:
(10х + у).
Утроенная сумма цифр этого числа будет иметь вид: (3(х + у)). =>
3(х + у) = 10х + у
Если поменять местами цифры искомого двузначного числа, то получим число: (10у + х). =>
10у + х - 45 = 10х + у.
Решим систему уравнений:
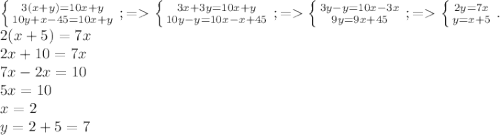
27 - искомое двузначное натуральное число.
Проверка:
3(2 + 7) = 27
3 * 9 = 27
27 = 27
72 - 27 = 45
V=(a-2x)(b-2x)·x
Исследуем функцию V(x) на максимум, минимум.
Находим производную
V=4x³-2ax²-2bx²+abx
V`(x)=12x²-4ax-4bx+ab
Приравниваем к ную
12х²-4ax-4bx+ab=0
12x²-(4a+4b)x+ab=0 квадратное уравнение относительно х:
D=(4a+4b)²-4·12·ab=16a²+32ab+16b²-48ab=16a²-16ab+16b²=16(a²-ab+b²)
x₁=(4a+4b-4√(a²-ab+b²))/24 или x₂=(4a+4b+4√(a²-ab+b²))/24
Расставим знаки производной
Производная квадратичная функция, график парабола, ветви вверх
+ _ +
-----------(х₁)---------------(х₂)---------------
Наибольшее значение в т.очке х₁, так как производная меняет знак с + на _
ответ. х=(4a+4b-4√(a²-ab+b²))/24