1) Найдем 3pi/4 в градусах так на много легче.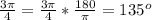
Имеем sin 135⁰ найдем через таблицу формулы приведения.
sin 135⁰ = sin (180 - 45) или sin (pi - 45) = смотрим = sin 45⁰ = 1/√2
ответ: sin 3pi/4 = 1/√2
2) cos 3pi/4 = cos 135 = cos (180 - 45) = -cos 45 = - 1/√2
3)tg 3pi/4 = tg 135 = tg (180 - 45) = -tg 45 = - 1
Тебе fse13написал
Sin 3pi/4= √2/2
Cos 3pi/4= - √2/2
это то самое √2/2 = 1/√2
Объяснение:
1)(2a - 5b)·(... - ...) = 6a^3 - 15a^2*b - 14ab + ...;
6a^3 : 2a = 3a^2
14ab : 2a = 7b
(2a - 5b)(3a^2 - 7b) = 6a^3 - 15a^2*b - 14ab + 35b^2
2)(... - ...)·(6x^2 - 5y^2) = 12x^3 + 42x^2*y - ... - 35y^3;
12x^3 : 6x^2 = 2x
-35y^3 : (-5y^2) = 7y
(2x + 7y)(6x^2 - 5y^2) = 12x^3 + 42x^2*y - 10xy^2 - 35y^3
3)(3a + 4c)·(... + ...) = 20ac + 8bc + 6ab + ...;
20ac : 4c = 5a
6ab : 3a = 2b
(3a + 4c)(5a + 2b) = 20ac + 8bc + 6ab + 15a^2
4)(... + ...)·(2a + 5b) = ... + 5ab + 8ac + 20b
Здесь опечатка, в конце должно быть 20bc
5ab : 5b = a
8ac : 2a = 4c
(a + 4c)(2a + 5b) = 2a^2 + 5ab + 8ac + 20bc
ответ:Данный урок мы посвятим решению типовых задач на построение графика функции . Вспомним определение квадратного корня.
Определение. Квадратным корнем из неотрицательного числа называется такое неотрицательное число , квадрат которого равен .
.
Изобразим график – это правая ветвь параболы (рис. 1).
Рис. 1.
На графике наглядно виден смысл вычисления квадратного корня. Например, если рассмотреть ординату 16, то ей будет соответствовать абсцисса 4, т. к. . Аналогично, ординате 9 на графике соответствует точка с абсциссой 3, поскольку , ординате 11 соответствует абсцисса , т. к. (квадратный корень из 11 не извлекается в целых числах).
Теперь вспомним график функции (рис. 2).
Рис. 2.
На графике для наглядности изображены несколько точек, ординаты которых вычисляются с извлечения квадратного корня: , , .
Примеры на преобразование графиков с корнями
Пример 1. Постройте и прочтите график функции: а) , б) .
Решение. а) Построение начинается с простейшего вида функции, т. е. в данном случае с графика (пунктиром). Затем для построения искомого графика график функции необходимо сдвинуть влево на 1 (рис. 3). При этом все точки графика сдвинутся на 1 влево, например, точка с координатами (1;1) перейдет в точку с координатами (0;1). В результате получаем искомый график (красная кривая). Проверить такой легко при подстановке нескольких значений аргумента.
Рис. 3.
Прочтем график: если аргумент меняется от до , функция возрастает от 0 до . Область определения (ОДЗ) при этом требует, чтобы подкоренное выражение было неотрицательным, т. е. .
б) Для построения графика функции поступим аналогичным образом. Сначала строим график (пунктиром). Затем для построения искомого графика график функции необходимо сдвинуть вправо на 1 (рис. 4). При этом все точки графика сдвинутся на 1 вправо, например, точка с координатами (1;1) прейдет в точку с координатами (2;1). В результате получаем искомый график (красная кривая).
Рис. 4.
Прочтем график: если аргумент меняется от до , функция возрастает от 0 до . Область определения (ОДЗ) аналогична предыдущему случаю: .
Замечание. На указанных примерах несложно сформулировать правило построения функций вида:
.
Пример 2. Постройте и прочтите график функции: а) , б) .
Решение. а) Этот пример также демонстрирует преобразование графиков функций, но только уже другого типа. Начинаем построение с простейшей функции (пунктиром). Затем график построенной функции смещаем на 2 вверх и получаем на рисунке 5 искомый график (красная кривая). Точка с координатами (1;1) при этом, например, переходит в точку (1;3).
Рис. 5.
Прочтем график: если аргумент меняется от 0 до , функция возрастает от 2 до . Область определения (ОДЗ): .
б) Также начинаем построение с простейшей функции (пунктиром). Затем график построенной функции (рис. 6) смещаем на 1 вниз и получаем искомый график (красная кривая). Точка с координатами (1;1) при этом, например, переходит в точку (1;0).
Это табличные данные.
Sin 3pi/4= √2/2
Cos 3pi/4= - √2/2
Tg 3pi/4= - 1