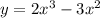
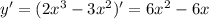
Необходимые условия экстремума:
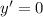
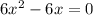
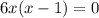

Имеем две критические (стационарные) точки:  и
и 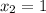
Достаточные условия экстремума: если при переходе через критическую точку производная непрерывной функции меняет знак на противоположный, то имеем экстремум функции в этой точке.
Если точка с абсциссой  меняет знак с "+" на "–" (двигаясь в направлении увеличения
меняет знак с "+" на "–" (двигаясь в направлении увеличения  ), то
), то  — точка максимума, а если с "–" на "+" , то
— точка максимума, а если с "–" на "+" , то  — точка минимума.
— точка минимума.
Из промежутка 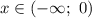 выберем, например,
выберем, например,  и имеем:
и имеем: 
Из промежутка 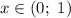 выберем, например,
выберем, например, 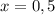 и имеем:
и имеем: 
Имеем максимум в точке с абсциссой 
Из промежутка 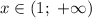 выберем, например,
выберем, например, 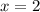 и имеем:
и имеем: 
Имеем минимум в точке с абсциссой 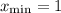
ответ: 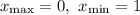
построй график квадратичной функции (порабола, ветвями вверх) далее, начитри данные в упрожнении... далее сам поймёшь
Находишьточки пересечения двух линий. Для этого решаешь ур.
x^2=4x+5. Получаешь х1=-1, х2=5
Теперь находишь разность интегралов
int(4x+5)dx-int(x^2)dx=2*x^2+5*x - x^3/3 в пределах (-1,5) и получаешь ответ 36