Question

Дорогу длиной 28км разделили на 3 неравные части. расстояние между серединами крайних частей равно 16км. найти длину средней части

Answer 1

Пусть наш путь - это сумма длин 3 неравных частей. Пусть это будут части с длинами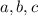 $a,b,c$

Известно, что общая длина равна 28 км. То есть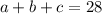 $a+b+c=28$

Крайние части - части с длинами $a$, $c$.

Середина делит часть пополам. А расстояние между серединами крайних частей затрагивает одну половину от $a$, одну половину от $c$ и всю $b$.

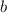Тогда получаем, что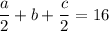 $$\frac{a}{2}+b+\frac{c}{2}=16$ км.

Из этого получается система:

$$\left \{ {{a+b+c=28} \atop {\frac{a}{2}+b+\frac{c}{2}=16 }} \right.$

Вычтем из первого уравнения системы второе, тем самым исключив b.

Получаем:

$$a+b+c-(\frac{a}{2}+b+\frac{c}{2})=28-16; a-\frac{a}{2}+b-b+c-\frac{c}{2}=12; \frac{a}{2}+\frac{c}{2}=12$

То есть $a+c=24$

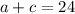
Мы знаем, что

$a+b+c=28; a+c=28-b \Rightarrow 24=28-b \Rightarrow b=4$ (км)

ответ: длина средней части дороги равна 4 км.

Answer 2

Длина средней части равна 4

Объяснение:

Пусть длины участков X, Y, Z.

Запишем два уравнения:

X + Y + Z = 28

X/2 + Y + Z/2 = 16

Или, домножив второе уравнение на 2, получим систему:

X + Y + Z = 28             (1)

X + 2Y + Z = 32           (2)

Из уравнения (2) вычтем (1)

Y = 4