см.рисунок
==============================================
Дана арифметическая прогрессия -15, -12, ..., то есть a₁= -15, a₂= -12. Тогда
а) её разность:
d = a₂ - a₁ = -12 - (-15) = -12 + 15 = 3.
б) формула n-члена этой прогрессии :
a(n) = -15+3·(n-1)
в) выясним, содержится ли в этой прогрессии число 12:
a(n) = 12 или
-15+3·(n-1) = 12
3·(n-1) = 12 + 15
3·(n-1) = 27
n-1 = 27:3
n = 9+1=10∈N
Содержится под номером 10.
г) Так как d=3 >0, то в этой прогрессии бесконечное количество положительных членов. В самом деле:
a(n) = -15+3·(n-1)>0
3·(n-1)>15
n-1>15:3
n>5+1
n>6
Начиная с 7-члена арифметической прогрессии все члены положительные. Так как множество натуральных чисел N бесконечно, то положительных членов арифметической прогрессии бесконечно.
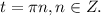 Если перебрать целые значения n, то получим числа:
Если перебрать целые значения n, то получим числа: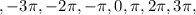 ....Это точки числовой окружности отмеченные, начиная с 0 через
....Это точки числовой окружности отмеченные, начиная с 0 через 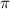 , (т е через полкруга). против часовой стрелки положительные значения, по часовой - отрицательные. Положительные значения из промежутка [0;2π] мы можем показать на окружности, таких значений два: 0 и
, (т е через полкруга). против часовой стрелки положительные значения, по часовой - отрицательные. Положительные значения из промежутка [0;2π] мы можем показать на окружности, таких значений два: 0 и 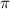 остальные будут совпадать с уже указанными, отрицательные значения из промежутка [-2π;0], их тоже два 0 и
остальные будут совпадать с уже указанными, отрицательные значения из промежутка [-2π;0], их тоже два 0 и 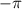 , для данной формулы тоже совпадут с уже указанными.
, для данной формулы тоже совпадут с уже указанными.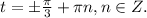 Это точки числовой окружности отмеченные, начиная с
Это точки числовой окружности отмеченные, начиная с 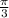 через
через 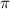 , (т е через полкруга) против часовой стрелки положительные значения, и начиная с
, (т е через полкруга) против часовой стрелки положительные значения, и начиная с  через
через 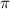 , (т е через полкруга) по часовой - отрицательные. И опять на промежутке [0;2π] мы можем показать на окружности только два значения:
, (т е через полкруга) по часовой - отрицательные. И опять на промежутке [0;2π] мы можем показать на окружности только два значения: 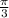 и
и 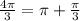 , остальные совпадут с уже указанными, и на промежутке [-2π;0] тоже два значения:
, остальные совпадут с уже указанными, и на промежутке [-2π;0] тоже два значения:  и
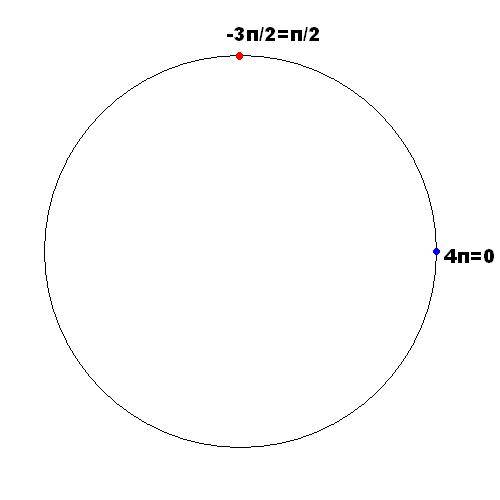
и 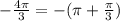 тоже совпадут с уже указанными.В целом мы отметили на окружности 4 точки:
тоже совпадут с уже указанными.В целом мы отметили на окружности 4 точки: 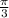 ,
, 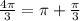 ,
,  ,
, 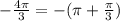 .
. 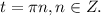 На промежутке [0;2π] два значения: 0 и
На промежутке [0;2π] два значения: 0 и 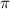 , остальные для
, остальные для 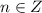 совпадут с уже указанными.
совпадут с уже указанными.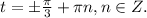 на промежутке [0;2π] два значения:
на промежутке [0;2π] два значения: 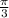 и
и 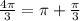 , на промежутке [-2π;0] тоже два значения:
, на промежутке [-2π;0] тоже два значения:  и
и 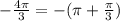 остальные для
остальные для 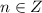 совпадут с уже указанными. Всего на окружности отмечено 4 точки:
совпадут с уже указанными. Всего на окружности отмечено 4 точки: 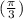 ,
, 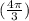 ,
, 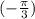 ,
, 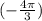 .
.
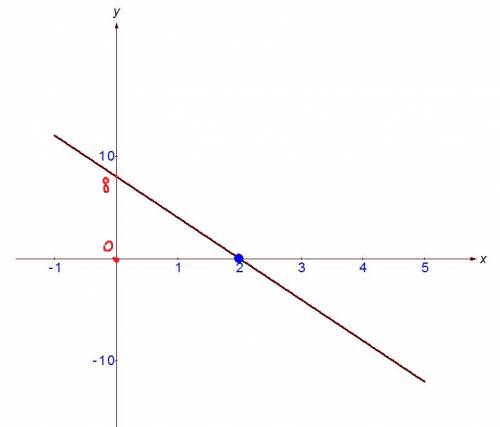
у=-4х+8
уравнение прямой, значит нужно две точки, чтобы её построить.
Берем х=0, у=8, то есть точка (0;8)
х=2, у=0, т.е. (2;0)
Чертим две прямые под углом 90 градусов.
отмечаем начало координат, единичный отрезок по каждой оси.
показываем положительное направление стрелками и отмечаем найденные точки.
проводим через них прямую линию, подписываем график.
Если нужно далее работаем с графиком.