Данное двойное неравенство равносильно системе двух квадратных неравенств:
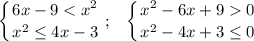
Первое неравенство  .
.
Заметим, что в левой части скрывается квадрат разности (формула  ):
): 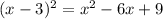 .
.
Неравенство принимает следующий вид: 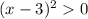 .
.
Так как квадрат числа всегда неотрицательный, то нам не подходит всего лишь один случай: 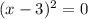 и
и 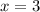 .
.
Значит, первой неравенство эквивалентно тому, что 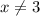 .
.
Второе неравенство 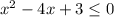 .
.
Вс уравнение 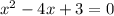 имеет по теореме Виета (утверждающей, что
имеет по теореме Виета (утверждающей, что 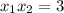 и
и 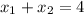 ) корни
) корни 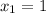 и
и 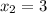 .
.
Из этого следует разложение левой части на множители: 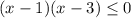 .
.
Метод интервалов подсказывает решение ![x \in [ 1; 3 ]](/tpl/images/1227/3957/60bcc.png) .
.
+ + + - - - + + +
_________![[ \; 1 \; ]](/tpl/images/1227/3957/d73a9.png) _________
_________![[ \; 3 \; ]](/tpl/images/1227/3957/abab5.png) _________
_________
\\\\\\\\\\\\\\\\\\\\\
Значит, второе неравенство равносильно тому, что  .
.
Имеем значительно более простую систему неравенств:

Вполне понятно, что ее решением является 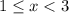 (как пересечения двух промежутков).
(как пересечения двух промежутков).
Или же 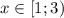 .
.
Задача решена!
ответ: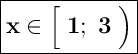
y=(x+2)^2-4 - квадратичная функция, график - парабола, ветви направлены вверх, график можно получить путём параллельного переноса графика функции y=x^2 на 2 единичных отрезка влево и на 4 единичных отрезка вниз
1) D(y)=R
2) Нули: x=0 при y=0; y=0 при x=0 и x=-4
3) y<=0 при x принадлежащем [-4;0], y>0 при x принадлежащем (-бесконечность;-4) и (0;+ бесконечность)
4) Функция убывает на промежутке x принадлежащем (-бесконечность;-2) и возрастает на промежутке x принадлежащем (-2;+ бесконечность)
5) E(y)=[-4;+бесконечность).
Подробнее - на -
Объяснение: