12см и 16 см
Объяснение:
1) Пусть одна сторона прямоугольника равна х см, тогда вторая - (х+4) см. Так как в прямоугольнике все углы прямые, найдём диагональ прямоугольника по теореме Пифагора:
х²+(х+4)²=20²
2х²+8х-384=0
х²+4х-192=0
D = 4²-4*(-192)=16+768=784=28²
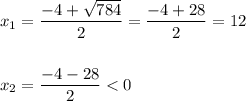
т.к. сторона не может быть меньше нуля, то меньшая сторона прямоугольника равняется 12см, большая: 12+4=16см
2) Если меньшую сторону обозначить через х см, а большую через у см, то получим следующие уравнения:
у-х=4 (одна сторона на 4 см больше от другой)х²+у²=20² (находим диагональ по т.Пифагора)Система уравнений, которая соответствует условию задачи:
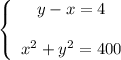

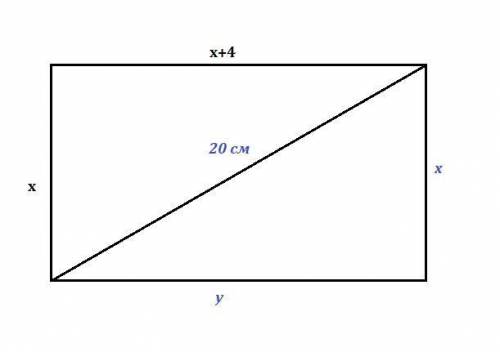
1)
У=-2х^2+5х+3
-4 =-2х^2+5х+3
-2х^2+5х+7 = 0
D = 25+ 2*7*4 = 25+56 = 81
корень из D = 9
х1 = (-5 +9)/(-4) = -1
х2 = (-5 -9)/(-4) = 3,5
2) (файл прикреплю)
а) y=9/4+3-8=5.25-8= -2.75
б) x^2-2x-11=0
x1=1+2√3
x2=1-2√3;
3) (от -∞ до -2] и [от 4 до +∞)
4) (от -∞ до 1]
3)
ибо ветви направлены вниз, то вершина параболы принимает наибольшее значение.
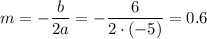
тогда, подставив х=0,6 в заданную функцию, получаем наибольшее значение функции:
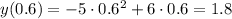
Наименьшего значения функции нет.
как то так наверное....
https://ru-static.z-dn.net/files/d0c/b840827e4223ecccede8572e809f0887.jpg