Алгебра: 7класс решите уравнение : 5х-6(5+2х)=х-2.

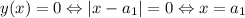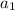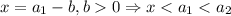
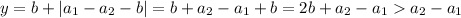
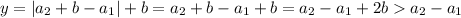
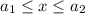
Если N четно, , а если нечетно, Объяснение:N=1: модуль не может принимать значения, меньшие 0. При этом - а значит и есть оптимальное [будем называть оптимальными искомые значения переменной] значение.N=2: Тут возможны 3 случая.1) Тогда 2) Тогда 3) Тогда Значит, оптимальными будут все значения .N=2k:Тогда функция представима в виде 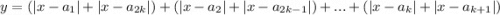.Для первого слагаемого оптимальными будут (как показано ранее) все точки отрезка .Для второго слагаемого оптимальными будут все точки отрезка . При этом, по условию,...

7класс решите уравнение : 5х-6(5+2х)=х-2.

👇

Увидеть ответ

Ответ:

Kutisheva2006

20.06.2020

5х-6(5+2х)=х-2
5х-30-12х=х-2.
5x-12x-x= 30-2
-8x = 28
x= 28÷(-8)
x= -3.5

4,6(50 оценок)

Открыть все ответы

Ответ:

4iksa12345ozu4gd

20.06.2020

Необходимо начертить единичную окружность и заставить точку "бегать" по окружности: 3П - это 1,5 круга, соответствует углу 180 градусам. Точка будет иметь координаты (-1,0). По определению sin и cos это и есть их значения: sin3П=0, cos3П=-1.
Аналогично: sin 4п=0, сos4П =1
sin3,5п=1, сos3,5П=0;
sin5/2П=1, cos 5/2П=0
sinПк=0 сosПк=1 (если к -четное ) и cosПк =-1 если к- нечетное число
(2к+1) - это формула нечетного числа, к примеру 3, 5, 7, 9 и т.д.
Следовательно, sin(2к+1)П=0, cos(2к+1)П =-1..

4,4(99 оценок)

Ответ:

plz11POMOGITE11plz

20.06.2020

Если N четно, $x\in\left[a_\frac{N}{2};a_{\frac{N}{2}+1}\right]$ , а если нечетно, $x=a_\frac{N+1}{2}$

Объяснение:

N=1: модуль не может принимать значения, меньшие 0. При этом $y(x)=0\Leftrightarrow |x-a_1|=0\Leftrightarrow x=a_1$ - а значит a_1 и есть оптимальное [будем называть оптимальными искомые значения переменной] значение.

N=2: Тут возможны 3 случая.

1) $x=a_1-b, b0 \Rightarrow x$

Тогда y=b+|a_1-a_2-b|=b+a_2-a_1+b=2b+a_2-a_1a_2-a_1

2) $x=a_2+b, b0 \Rightarrow a_1$

Тогда y=|a_2+b-a_1|+b=a_2+b-a_1+b=a_2-a_1+2ba_2-a_1

3) $a_1\leq x\leq a_2$

Тогда y=x-a_1+a_2-x=a_2-a_1

Значит, оптимальными будут все значения $x\in [a_1;a_2]$ .

N=2k:

Тогда функция представима в виде $y=(|x-a_1|+|x-a_{2k}|)+(|x-a_2|+|x-a_{2k-1}|)+...+(|x-a_k|+|x-a_{k+1}|)$ .

Для первого слагаемого оптимальными будут (как показано ранее) все точки отрезка $[a_1;a_{2k}]$ .

Для второго слагаемого оптимальными будут все точки отрезка $[a_2;a_{2k-1}]$ . При этом, по условию, имеем $[a_2;a_{2k-1}]\subset [a_1;a_{2k}]$ - то есть все точки этого отрезка оптимальны и для первого слагаемого

...

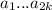Для k-ого слагаемого оптимальными будут все точки отрезка $[a_k;a_{k+1}]$ . При этом $[a_k;a_{k+1}]\subset [a_{k-1};a_{k+2}]\subset...\subset [a_1;a_{2k}]$ - то есть все точки этого отрезка оптимальны и для остальных слагаемых. Но тогда все точки этого отрезка являются оптимальными для всего набора $a_1...a_{2k}$ .

N=2k+1:

Тогда функция представима в виде

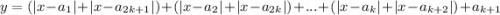$y=(|x-a_1|+|x-a_{2k+1}|)+(|x-a_2|+|x-a_{2k}|)+...+(|x-a_k|+|x-a_{k+2}|)+a_{k+1}$ .

Проведя k шагов аналогичных рассуждений, получим, что для набора 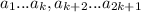$a_1...a_k,a_{k+2}...a_{2k+1}$ оптимален отрезок $[a_k;a_{k+2}]$ .

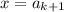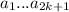Для $a_{k+1}$ , как показано ранее, оптимально значение $x=a_{k+1}$ . При этом $a_{k+1}\in[a_k;a_{k+2}]$ - то есть это значение оптимально и для остальных слагаемых. Но тогда оно оптимально для всего набора $a_1...a_{2k+1}$ .