1 C
2 A
3. 40√6
4 √14 , 3√2, 23
5. 2√11
6. пройдет
Объяснение:
2. Возведем в квадрат √ и границы интервалов и увидим
3. √96100 = √(6*16*100) = 40√6
4. возведем в квадрат: 14, 529, 18
5. 22/√11 = 2√11√11 / √11 = 2√11
6. так же возведем в квадрат H² = 32, h² = 29.16 h<H пройдет
7. = 3* (3-√b- 3 -√b) / (9-b) - 2b/ (9-b) = (6√b+2b)/b-9 = 2√b(3+√b)/(9-b)
непонятно зачем там про а сказано...
8. а) √а = 8√3
√а = √192
а = 192
b) √0 = 0, √36 = 6
у ∈ [0;6]
c) 14² = 196
28² = 784
x ∈ [196; 784]
d) y≤5
√x≤5
x ≥0
x≤ 25
x ∈ [0;25]
1.
p=34cm
a=x
b=x-3
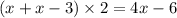
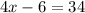

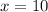
Длина 10, Ширина 10-3=7
2)
Известно, что туристическую группу из 38 человек расселили в двухместные и трёхместные номера.
При этом всего было занято 14 номеров.
Требуется вычислить сколько среди них было двухместных и сколько трёхместных.
Обозначим количество двухместных номеров "х", а количество трёхместных "у".
Тогда:
х + у = 14
х = 14 - у.
Составим уравнение.
2х + 3у = 38,
Подставим значение "х".
2 * (14 - у) + 3у = 38,
28 - 2у + 3у = 38,
у = 38 - 28 = 10 трёхместных номеров.
14 - 10 = 4 двухместных номеров.
на втором 72 (множ-во Б)
на третьем 60 (множ-во С)
пусть во множество Б вошли 20 учеников плохо сдавших первый экзамен, и соответственно 52 человека которые сдали 1 и 2 экзамен хорошо.
Таким образом, 20 учеников не сдали ни первый ни второй экзамен
52 сдали 1 и 2 экзамен
28 сдали хорошо только один из двух первых экзаменов.
Пусть третьий экзамен сдали хорошо 20 человек не сдавших 1 и 2 экзамен, 28 человек сдавших один из двух первых экзаменов (уже 48) и значит 12 человек сдавших и первый и второй экзамен хорошо.
Таким образом сдали все три экзамена на хорошо и отлично только 12 человек, а это 12%