Чтобы найти квадратный корень из степени неотрицательного числа, просто умножьте показатель степени подкоренного выражения на ½ (или разделите на 2).
Пример.
√(2²) = 2^( ½ * 2) = 2^1 = 2
26,
т.к. по условию в графу ответа надо писать
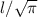
Объяснение:
Из условия ни разу не ясно, что есть такое некая непонятная "его длина".
Но по всей видимости,
а) это диаметр условной окружности, которую образует Кольцевая линия.
б) это (ну, блин, грамотеи!) длина окружности, которую образует Кольцевая линия.
а) Найдем диаметр условной окружности, которую образует Кольцевая линия.
Обозначим её как d.
Площадь Центрального района S можно вычислить следующим образом:
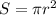
где r - это радиус условной окружности Кольцевой, или половина диаметра, т.е. d/2. Отсюда.
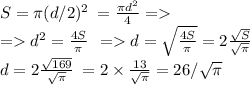
б) Найдем длину окружности, которую образует Кольцевая линия. Обозначим её как l.
Длина окружности равна
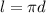
где d - условный диаметр (см. (а)).
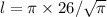
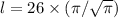
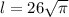
Согласно требованиям задачи в ответ записываем
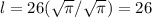
т.е.
ответ: 26
квадратный корень, оно потому и квадратный, т.к.=числу извлеченному из степени 2,
название пошло от площади квадрата, т.к. площадь квадрата=произведению его длины и ширины, а они одинаковы
т.е корень из 4=корню 2*2=числу 2
любой корень квадратный можно принять как основание со степенью 1/2, если можно разложить число в степень, например, 3*3*3*3=3⁴=81, то квадратный корень из этого числа =3в степени(4*1/2)=3в степени (2)=3*3=9